Graphs -- 1 variable

Return to Topics

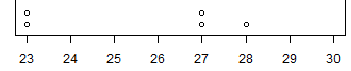
The objective of this page is to present, in the most elementary way, some of the one variable graphs that we find or use in elementary statistics. Links are provided to other pages that demonstrate creating these graphs in R.


As a small but significant disclaimer, please note that R has at least three completely separate, and to some extent, redundant systems for creating graphs, charts, and plots. These pages only use the base plotting system. We expect that this base system to be more than sufficient for our needs. However, should you ever need fancier graphs, rest assured that R is quite capable of producing them, though maybe through the other two systems.

On this page we will take a quick look at

Bar Chart

 A bar chart is used to show the relative size of discrete values. For example, if we have the values
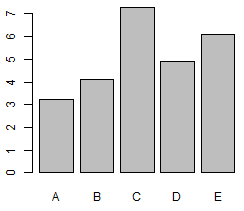
Table 1
Label A BCDE
Value 3.24 4.13 7.3 4.9 6.1
we could picture those values as
Figure 1


Notice that these are discrete values. The bar chart reflects this "discrete" attribute by actually separating the bars, that is, there is space between the bars. [This is different than what we will see in a histogram.]

The bars in Figure 1 are vertical but we could produce the same information in a horizontal format, as in Figure 2.
Figure 2


A bar chart can be in either vertical or horizontal format. The bar charts shown above give you a "feeling" for the relative size of the values.

A more common use for a bar chart is to show the relative frequency of lots of discrete values. Consider the values in Table 2, a table of values that you can create in R using It is almost impossible to get a feel for those values just by looking at them. There are just too many! However, if we create a bar chart showing the frequency of the different values in that table, then, from such a chart, we get an immediate impression of the distribution of those values. Look at Figure 3.
Figure 3


Clearly, the lower values happen much more often than do the upper values. In fact, just looking at the bar chart, it is clear that the mode value is 23. With a little consideration, and knowing that there are 94 values in the table, we see that the median value is going to be the average of two of the 25's, so the median will be 25. We also can see that the range is values from 23 to 30,

See the page Making Bar Charts in R for a more detailed discussion of how you can create bar charts in R.

Histogram

 A histogram is used to show the distribution of continuous values, or the distribution within groups of discrete values. Let us look at an example of the latter first. Table 3 has discrete values, ones you could generate in R using

we could take a quick look at the values in the table by doing a summary of the values:
this shows us that those values cover a lot of territory, namely, we have 95 values in the range from 27 to 97. We could use a bar chart to look at the frequency of each value, but there would not be a high frequency of any one value and we would have a different bar for each different value. Here is such a bar chart.
Figure 3.5


That bar chart is just too busy; it has too many bars to be of real use. However, it is clear that the values in Table 3 are all between 20 and 100. What if we create "bins" ("or "clusters" or "cells" or "buckets") where we have a "bin" for the values from 20 to 30, another for values between 30 and 40, another for the values between 40 and 50, and so on until our last "bin" is for values between 90 and 100. Then, with those eight "bins" we could report the number of values from Table 3 that fall into each "bin". That is what a histogram does. Figure 4 shows such a histogram.
Figure 4




Just a glance at Figure 4 tells us that there are more high values in Table 3 than there are low values. Although we have no idea what value happens the most often in Table 3, we can see that there are more values in the 70 to 80 bin than in any other bin. [Interestingly enough, the individual values that appear most often in the table are 80, 91, and 93, each showing up 5 times.] Also, knowing that there are 95 values in the table, the median value will have to be in that same bin because there are only 40 values above that bin and there are more than 20 values in that bin, meaning that there are less than 30 values below it.

Note that in a histogram we have the rectangles adjacent to each other. In fact, that adjacency points us to an important question: If the first bin holds values from 20 to 30, and the second holds values from 30 to 40, then which bin gets the value 30? In R the default in making a histogram considers "20 to 30" to mean "greater than 20 and less than or equal to 30". Therefore, the value 30, which is in the data collection, goes into the bin of values from 20 to 30. We can change that default behavior and have the 20 to 30 interval mean include 20 and everything up to but not including 30 and get a slightly different graph, as shown in Figure 4a.
Figure 4a


That small change in the definition made a noticeable change in the graph. [There are 2 values in the table less than 30 and two values of 30. That distribution causes the change in the left end of the graph.] Naturally, we should note the choice of including the left or right endpoints somewhere, if we are going to be publishing the histogram or even if we are going to ask someone else to look at it. If you encounter a histogram, especially one for groups of distinct values, you should determine which end of the interval is included and which is not.

You might also note that the width of the bins is the same for all of them. This is important.

As noted above, we often use a histogram to portray the distribution of continuous values. Now our continuous values are not really continuous in the sense that that we have infinite precision. Any values that we use will be rounded to some number of decimal places. If we have measurements that are given to two decimal places then we cannot have a value between, for example, 23.14 and 23.15 are values, there is no way for us to have another value between them. Nonetheless, if we have continuous values and we record approximations to them to some number of decimal places, then we still consider them to be continuous. Let us look at the values in Table 4, values that you can produce in R by using

If we look at a histogram of those values, Figure 5, we get a quick idea of the distribution of the values in Table 5.
Figure 5

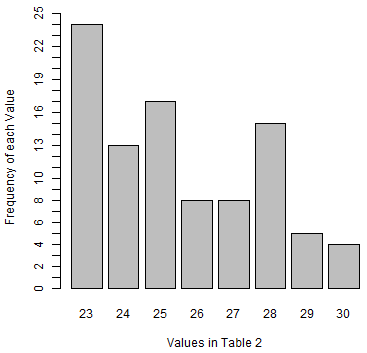
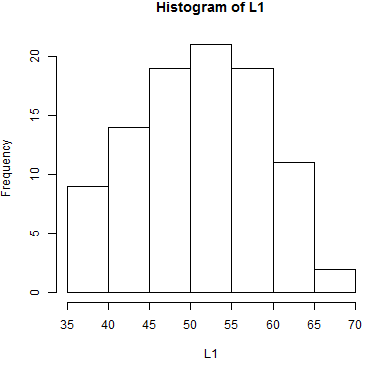
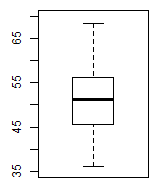
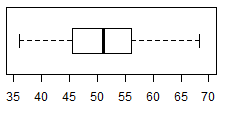
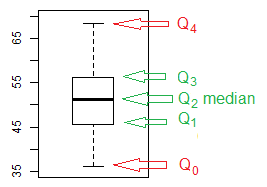
In particular, we see that the values must be between 35 and 80, and that most of the values appear near the middle of that range with fewer values at the extremes. In fact, of the 95 value in the table, only 2 appear to be greater than 65 and only 9 appear to be less than or equal to 40, assuming the histogram was produced using the default R settings.

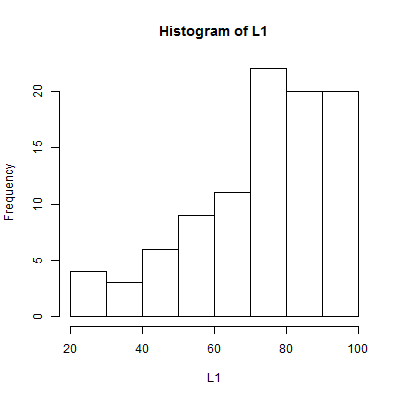
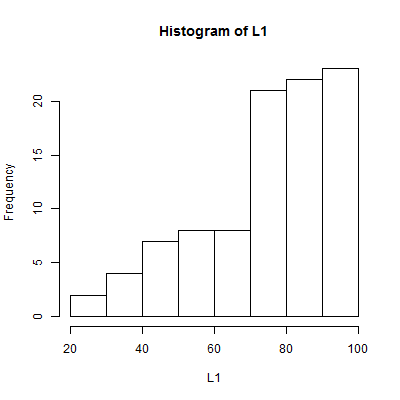
One aspect of making a histogram is deciding how many bins you will use and where the breaks between the bins will fall. In Figure 5 there are 7 bins starting at 35 and having a width of 5. What if we keep the 7 bins but we change the breaks between the bins? One version of that is shown in Figure 6.

Figure 6


Remember that the data in Table 4 is used to generate both Figure 5 and Figure 6. However, the image of the distribution of that data is different in the two figures. And, depending upon the viewer, the two figures may give a different impression of the distribution of the values in the table.

This same change in impressions can arise from increasing, or decreasing, the number of bins. In Figure 7 we have a histogram of the same data, but this time we have twice as many bins.
Figure 7


On the other hand, in Figure 8, we show the same data but this time with only 4 bins.
Figure 8


There is no magic formula that will tell us the "correct" number of bins or the "correct" break points to use. It is important to be aware of the fact that when we choose values for those parameters we are influencing how the histogram appears.

See the page Making Histograms in R for a more detailed discussion of how you can create histograms in R.

Box and Whisker

Box and Whisker charts give a different view of the distribution of values in a data set. In this case the chart represents a standardized approach to looking at the position of the quartile points for the data. As a first example we will continue to use the data in Table 4. A box and whisker chart for that data is given in Figure 9.
Figure 9


or, in a horizontal version as Figure 9h
Figure 9h


To help explain the box and whisker plot, I have annotated Figure 9 as Figure 10.
Figure 10


The rectangle in the middle of the chart shows the relative position of Q1, Q2, and Q3. In our particular example, we get the idea that Q2, the median, has a values somewhere around 50, while Q1 has a value around 45 and Q3 has a value around 55. [If you were to use the summary(L1) command you would find that Q1=45.61, Q2=51.11, and Q1=56.15.] The box chart is showing us the spread of the values. We get a good idea that the width of the second and third quartiles is approximately the same.

Then, in Figure 10, we see the whiskers reach down to Q0 and up to Q4, the minimum and maximum values respectively. From this we can see that there is a greater spread of the values in the first and fourth quartile than we saw in the second and third quartiles. It is important to remember that we have about a quarter of the values in each of the quartiles.

As it turns out, the data we have been using, the values in Table 4, are relatively symmetric in their distribution. Let us look at a different collection of data, that in Table 5, values that you can produce in R by using

A box and whisker chart for the data in Table 5 is given in Figure 11.
Figure 11


From that figure we can see In order to understand the lower portion of Figure 11 we have to introduce a new concept, the interquartile range, the IQR. The IQR is just the difference between Q3 and Q1, in Figure 11 that would be about 63-57 or, approximately, 6.

The Box and Whisker charts shown here allow the whiskers to extend no more than 1.5*IQR above Q3 and below Q1. The maximum value in Table 5 is 67.2. That means that drawing the whisker from Q3 to Q4 would result in a whisker that is shorter than 1.5*IQR. Therefore, we draw that whisker. However, the lowest value in Table 5 is 42.8 and if we were to draw a whisker from Q1, about 57, to that minimum value,Q0, the resulting whisker would be about 14 units long, longer than 1.5*IQR. That is not allowed. Instead, the lower whisker is drawn from the rectangle to the lowest data point that is still within 1.5*IQR of Q1, and any value beyond that whisker is shown as an individual point. In Figure 11 the lower whisker is extended for a to 48.9, the lowest data value that is still within 1.5*IQR of Q1. The one value in Table 5 that is lower than Q1-1.5*IQR is shown by the small circle in the plot.

Values that are above Q3+1.5*IQR or below Q1-1.5*IQR are considered outliers, that is, they are values that are extremely different from other values in the data collection. Being an outlier does not mean that we should just throw out the value. It does mean that we should at least look at the value to see if it is indeed valid.

How can a data value be "invalid" you ask. There could have been a clerical error in entering the data. A device that collects the data may have malfunctioned or could have experienced a situation for which it was not designed. Our procedure for identifying our population may have not been strict enough and some non-representative items may have been included. Using the 1.5*IQR value seems to be a good way to identify such outliers.

The box and whisker chart in Figure 11 gives us a good picture of the distribution of values that we saw in Table 5. It gives us a "feeling" for the data, and probably a more complete "feeling" than we would get if we just looked at the numbers giving us the exact values of the quartile points. For completeness, Figure 11s shows those values.
Figure 11s


Also, because both vertical and horizontal charts are common, here is a horizontal version of the previous chart.
Figure 11h


See the page Making Box and Whisker Charts in R for a more detailed discussion of how you can create Box and Whisker Charts in R.

Pie Chart

A pie chart is used to show the relative size of a small group of values. For example, if we have the values
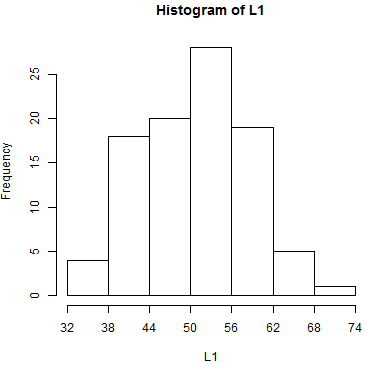
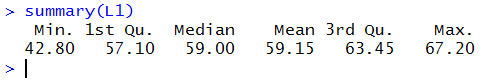
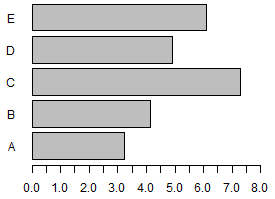
Table 6
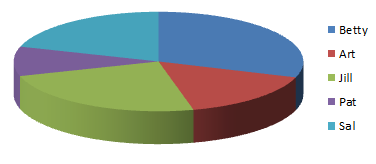
Label Betty ArtJillPatSal
Value 9.13 4.82 7.3 2.9 6.1
we could picture those values as
Figure 12


We teach making pie charts starting in elementary school. It would seem that we do this because making a pie chart involves so many arithmetic skills as well as using the fact that a circle has 360°, and the skill of using a compass, a protractor, and a straight-edge. That knowledge and those skills have been undermined by software that just generates pie charts for us. The pie chart in Figure 12 was created by R with almost no effort. We could have used Excel to do the same thing. Figure 13 and Figure 14 show pie charts created for the same data in Excel.
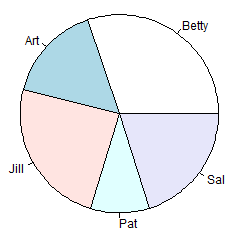
Figure 13Figure 14


The problem with pie charts is two-fold. First, people are really not good at distinguishing differences based on angles and non-rectangular areas. For that matter, we have a hard time judging areas unless they have a common width. That is why we have equal width rectangles in both bar charts and histograms. (See "old people" page for a small, real world, illustration.) The second problem is that it is really easy to strongly suggest a wrong impression using pie charts, especially the fancy 3-D ones, an instance of which is shown in Figure 14. The immediate, and obvious when you think about it, concern is that by showing part of the edge as in Figure 14 the chart presents even more "shaded area" for a piece of the pie than it deserves. In Figure 14 we see not only the top of the green sector but also the side, also shaded green. However, we only see the top of the blue sector.

In general, it is important to know how to produce a pie chart but in practice you should avoid using them.

See the page Making Pie Charts in R for a more detailed discussion of how you can create Pie Charts in R.

Dot Chart

We will present the dot plot here because it is part of the course and for historical reasons. In the form associated with this course the dot plot no longer has any practical application unless you suddenly lose access to a computer. To illustrate a dot plot let us return to Table 2 which we will repeat here.

You construct a dot plot by placing the distinct data values along the x-axis of the chart. Then, as you go through the data values, each time you find a value you place a new dot above the value in the x-axis of the chart. Thus, for the data in Table 2 we see that we have values from 23 to 30. Therefore, we start with an x-axis that has values from 23 through 30, as in
Then, we start going through the data values. The first is 23 so we put a dot above 23. The second is another 23, so we put a dot above the dot that is already above 23. The third value is 28 so we put a dot above 28. The fourth value is 27 so we put a dot above 27. The fifth value is another 27 so we stack another dot above 27. At that point our plot looks like
And then we just keep going. In the end we will have as many dots above 27 as there are 27's in the data. The completed dot plot would appear as
Figure 15


If you compare this to Figure 3 (repeated below) you will find that the dot plot is really a bar chart but with dots instead of bars.
Figure 3 - repeated


This leaves us with the question of why do we even have such a thing as a dot plot? It is simply a historical artifact. If we did not have a computer, if we did not have a nice way to even sort the data values, if we were just given the data values and a blank sheet of paper then we could construct a dot chart right from the data and we could do that without even sorting the data values. We end up with a chart from which we could actually get a count of the each of the distinct values, that is a frequency for the data values. However, once we have a computer and a bit of software, especially software that can construct a bar chart, there is no need for a dot plot.

R does not have a dot plot function as described here, but that does not mean that we cannot teach R how to make one of these dot plots. As you may have guessed, that is exactly what I did to create Figure 15. Should you actually need to create a dot plot, then you should see the page Making Dot Plots in R for a more detailed discussion of how you can create Dot Plots in R.
Return to Topics

©Roger M. Palay     Saline, MI 48176     October, 2015