| | |
Systems of Two Linear Equations
Ax + By = C
Dx + Ey = F
where A, B, C, D, E, and F are numeric
|
|
| |
| | |
|
| |
No solution; the graphs are parallel
This is called Inconsistent |
| |
| One solution; the graphs cross |
|
|
Infinite solutions; the graphs coincide
This is called Redundant or Dependent |
|
Example 1:
6x + 8y = – 40
3x + 4y = 12
|
| |
Example 2:
1x – 4y = 20
3x + 4y = 12
|
|
|
Example 3:
6x + 8y = 24
3x + 4y = 12
|
|
|
| |
|
|
|
|
| |
|
|
|
| | |
|
| |
| | |
|
| |
| | |
|
| |
| | |
| What to do if there are more equations than there are variables. |
|
| |
No solution; the graphs do not all
intersect in one point
This is called Inconsistent |
| |
| One solution; the graphs cross in one point |
|
|
Infinite solutions; the graphs coincide
This is called Redundant or Dependent |
|
Example 4:
3x – 2y = – 23
1x + 1y = – 1
4x – 1y = – 19
|
| |
Example 5:
4x – 3y = – 17
2x – 7y = – 25
5x + 4y = 2
|
|
|
Example 6:
3x – 5y = – 6
9x – 15y = – 18
6x – 10y = – 12
|
|
|
| |
|
|
|
|
| |
|
|
|
Example 7:
2x – y = 3
x – 2y = – 3
x – 2y = – 9
|
| |
Example 8:
7x – 4y = 5
9x – 10y = – 1
21x – 12y = – 15
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
| | |
Linear Equation in 3 variables
General form: Ax + By + Cz = D
is not a line but rather a plane |
|
| |
| | |
Example 9:
3x + 4y + 2z = 12
|
|
| |
|
|
|
| |
|
|
| | |
Example 10:
3x + 4y + 2z = 12
6x - 4y - 3z = 5
|
|
| |
|
|
|
| |
|
|
| | |
Example 11:
3x + 4y + 2z = 12
6x - 4y - 3z = 5
5x + 7y -12z =5
|
|
|
Matrix representation: Augmented Matrix
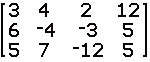
|
|
|
|
|
|
|
|
|
| |
|
|
|
| | |
Linear Equation in 4 variables
Switch to general symbols before we run out of them.
General form: C1x1 + C2x2 + C3x3 +C4x4 = K
is not a line, not a plane but rather a hyper-plane |
|
| |
| | |
Example 12:
-5x1 + 7x2 + 9x3 - 11x4= 56
1x1 + 2x2 - 6x3 - 3x4= 115
12x1 - 4x2 + 3x3 + 8x4= - 74
5x1 - 7x2 - 1x3 + 4x4= - 73
|
|
|
Matrix representation: Augmented Matrix
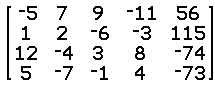
|
|
|
| |
|
|
|
|
| |
|
|
|
|
| |
|
|
|