Solve Earlier Examples By rref(

Return to Roadmap 2

Once we have seen how to use rref( it becomes quite easy to solve, or attempt to solve, systems f linear equations. Back on the Roadmap page for Chapter 2, before tackling Example 13, we used Examples 1, 2, 3, and 11. We will repeat working those examples here but using rref(.

Figure 1	Figure 1 shows the matrix representing Example 3, along with the result of running rref( on that matrix. This is far easier to do than solving by substitution, by addition, or by using the elementary row operations.
Figure 2	Figure 2 holds the matrix representing Example 2 abd the rref( solution to that problem.
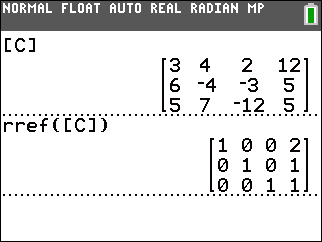
Figure 3	Figure 3 holds the matrix for Example 1. Recall, from the earlier page, that Example 1 demonstrated a case where there was no solution. The two lines that represent the two equations would be parallel if graphed. Therefoe there would be no point on both lines, or, there is no ordered pair that satisfies both equations. Our rref( result, shown at the bottom of Figure 3, indicates this by the impossible equation represented by the last line of the matrix In particular, if we used the values of that last row as the numeric values in our equation we would have `0x + 0y = 1` and there are no values that we coud use for x and y that will make this true. Therefore, we understand that if the last line of the matrix represents an equation with no values that make it true, then the system of linear equations has no solution.
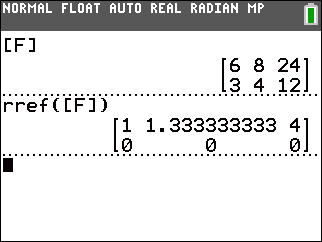Figure 4	Figure 4 holds the matrix representing the equations in Example 3. Recall, from the earlier page, that Example 3 demonstrated a case where there are infinitely many solutions. The two equations, if graphed, would be the same line. Our rref( result, shown in Figure 4, indicates this by having the values that, if translated back to an equation, would make that equation true for all values. Thus, the final row of the matrix, if brought back to equation form, would look like `0x + 0Y = 0`, n equation that is true no matter what values you choose for x and y. Therefore, we understand that if the final row in the matrix is all 0's then there are infinitely many solutions to the original system of linear equations.
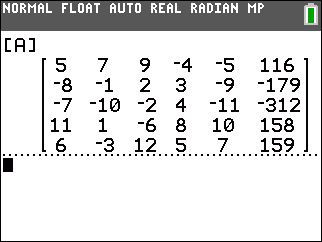Figure 5	Finally, just as a small treat, Figure 5 holds the matrix for a system of 5 linear equation in ive variables. This is the kind of problem that used to be given as a take-home exam in math classes. To solve it by substitution, by addition, or even by elementary row operations takes an inordinat amount of time and effort. The chance of getting the problem wrong because of some arthmetic error is quite high.
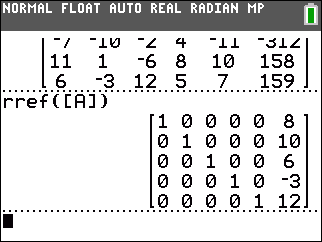Figure 6	We solve the problem shown in Figure 5 by the simple rref( command shown in Figure 6. The result, assuming tht the variables were x₁, x₂, x₃, x₄, and x₅ is that x₁ = 8, x₂ = 10, x₃ = 6, x₄ = ^–3, and x₅ = 12.