Solve By Elementary Row Operations

Return to Roadmap 2

We will solve Example 11 from the Chapter 2 Roadmap page by using elementary row operation. Start with the initial system of three linear equations in three variables.

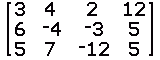
3x + 4y + 2z	=	12	(1)
6x – 4y – 3z	=	5	(2)
5x + 7y – 12z	=	5	(3)

Once we make sure that we have accounted for all of the variables in all of the equations and that the variables are in the same order in all equations, we can represent that system of linear equations via the matrix

There are a few important aspects of having the system of linear equations. First, there was no special order to the equations. We could have rearranged the order but in doing so we would end up rearranging the order of the rows in the matrix. Second, we could have multiplied any of the equations by a non-zero constant. That would change the form of the equation but not the set of points that satisfy the equation. Of course, in the matrix this would correspond to multiplying the affected row of the matrix by that same constant. And third, we could multiply, off to the side, any equation in the system by a non-zero constant and then add the resulting equation to either of the other equations in the system. In the matrix this amounts to multiplying, off to the side, a row of the matrix and then adding that result to a different row of the matrix. Those three actions are captured by three elementary row operations, rowSwap, *row, and *row+. These are built-in functions of the TI-83/84 family of calculators. The nane, syntax, and semantics of the three is given in the following table.

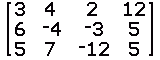
name	Syntax	Non-TI Symbols	Semantics
rowSwap(	*rowSwap(matrix name, row1, row2)*	R_row1 ↔ R_row2	Interchange row1 with row2 in the identified matrix.
*row(	row(value, matrix name, row1*)	valueR_row1 → R_row1	Multiply each number in row1 of the identified matrix by the given value..
*row+(	row+(value, matrix name, row1, row2*)	valueR_row1 +R_row2 → R_row2	Off to the side, multiply each value of row1 of the designated matrix by the given value. Then add the resulting numbers to the numbers in row2 of the matrix. Row1 is not changed.

We will use those commands to do the elementary row operations on our calculator.

The calculator used to make the images on this page was a TI-84 Plus C. It has more resolution on the screen than do the older models in the TI-83/84 calculator. In addition, the calculator used here uses the MATHPRINT, rather than the CLASSIC option. The result is a matrix that looks more like a matrix. If you are using an older calculator, or using one in the CLASSIC mode, you will have to make some adjustment for the change in the display. However, the computations will be identical.

The process here is to change, in a step by step fashion, the given matrix to one that has 1's down the diagonal and 0's below and above those 1's. If you skip down to Figure 15 you will see that goal expressed as

This matrix, in turn, really represent three linear equations, namely,

1x + 0y + 0z	=	2	(4)
0x +1y + 0z	=	1	(5)
0x + 0y + 1z	=	1	(6)

But that is the solution, x=2, y=1, and z=1 which can be expressed as the point (2,1,1).

We just need to see the steps to go from the matrix

to the matrix

Figure 1	To get the matrix into the calculator we use the key sequence. This opens the window shown in Figure 1.
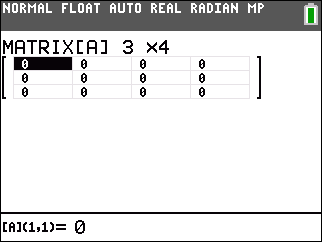
Figure 2	We will put the matrix into one of the ten defined matrices. For this example we will use the [A] matrix. We use the keys to move the highight to the EDIT option, as is shown in Figure 2. Because the [A] matrix is already selected we can just press the to ask the calculator to edit matrix [A].
Figure 3	On this calculator we did not have a prviously defined value in [A]. Therefore, Figure 3 shows [A] as a matrix with 1 row and 1 column.
Figure 4	Pressing changes the calculator matrix editor from the image shown in Figure 3 to the one shown in Figure 4. Now we need to fill in the values from our original equations.
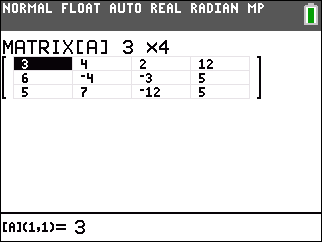Figure 5	Figure 5 shows all of the values in the appropriate spots of the matrix. We can leave Figure 5 and return the the home screen via the key sequence . Now we are ready to start the pocess described above. First we want to use the elementary row operations to create a 1 in the first row, first column spot. There are many ways to do this. One way is to note that the first item in rows 2 and 3 are different by 1. If we swap the first and second row, then we will have a 6 in the first row, first column position. Then, we can add – 1 times the third row to the first row to make row 1, column 1 hold the value 1. Our plan starts with swaping the first and second row. to do this we need to find the rowSwap( command. Press the to return to the main MATRIX page, then press to look at the MATH functions.
Figure 6	Figure 6 shows the list of the matrix MATH funtions. Our desired function, rowSwap( is not to be found in Figure 6. However, if we move down the listing, using the key many times, we will get to the functions shown in Figure 7.
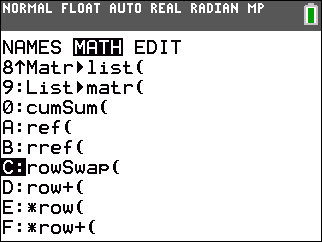Figure 7	In Figure 7 we see the rowSwap( option, and we have highlighted it. Then press the key to paste that option onto the main screen, as is shown in Figure 8.
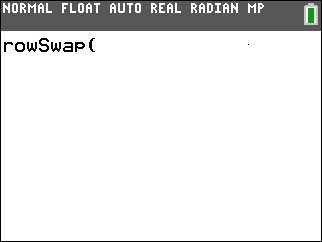Figure 8	Recall that the syntax for this command is *rowSwap(value, matrix name, row1). We want to swap rows 1 and 2 in matrix [A]. Therefore, the desired command is rowSwap([A],1,2)*. We construct that command, getting the matrix name from the matrix menu, and then press the key. The reuslt is shown in Figure 9.
Figure 9	It is important to note that the command has been performed. It worked just as we expected, the first and second rows of the matrix have been swapped. However, the resulting matrix, the one shown in Figure 9, is stored in Ans not in [A}. In fact, the contents of [A] are unchanged.
Figure 10	The next step is to multiply, on the side, row 3 of the matrix by ^–1 and then add that result to row 1. The command to do this is row+(^‐1,Ans,3,1). form this command we would have to return to the matrix functions list and elect the row+( option, then use the keys to continue the command. Follow that by to generate the Ans, then use to complete the command. Once constructed, press to run the command. All of this appears at the bottom of Figure 10.
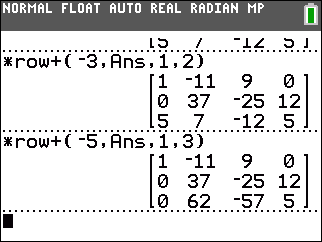
Figure 11	The next number of images continue the steps of the process. In each case, we return to the matrix function list to select the command we want and then we complete the command following the prescribed syntax. In all of these steps we continue to work on the matrix stored in Ans and each command produces a new result that is then stored in Ans. The top command in Figure 11 multiplies, on the side, the top row by ^–3 and adds it to the second row, thus creating a 0 in row 2, column 1. The next command multiplies, on the side, the top row by ^–5 and adds it to the third row, thus creating a 0 in row 3, column 1. At the end of Figure 11 we have finished the first column. Our next challenge is to get a 1 in row 2, column 2. That cell currently contains 37.
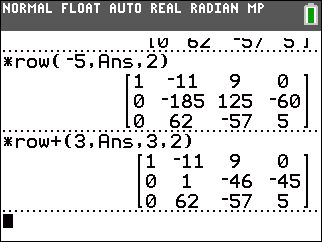Figure 12	It may seem a little obtuse, and it is, but I happen to know that 537 is 185 and that 362 is 186. Those values differ by 1. So, we multiply row 2 by ^–5, using the *row( function, and then multiply, on the side, row 3 by 3 and then add that result to row 2. The result appears in the lower portion of Figure 12. We have the desired 1 in row 2, column 2. This obtuse approach is handy in that it did not require using fractions. We could have manufactured the 1 from the original 37 by multiplying row 2 by 1/37. However tht would hae introduced fractions and I prefer to avoid them for now.
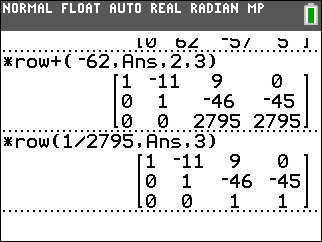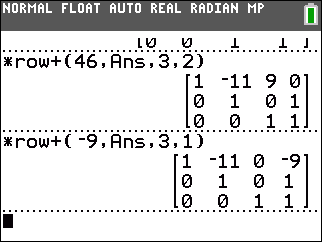Figure 13	At the top of Figure 13 we multiply row 2 by ^–62 and add the result to row 3, generating a 0 in row 3 column 2. In the lower portion of Figure 13 we multiply row 3 by 1/2795 generating a 1 in row 3, column 3. 1's down the diagonal and 0's below the diagonal. The next steps get 0's above the diagonal.
Figure 14	Multipy row 3 by 46 and add it to row 2. Multiply row 3 by ^–9 and add it to row 1.
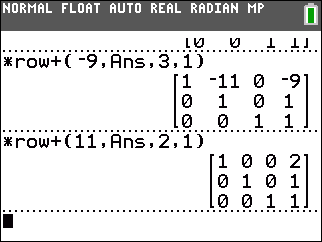Figure 15	The upper portion of Figure 15 is just the lower portion of Figure 14. The new command in Figure 15 is to multiply row 2 by 11 and add it to row 1. The fianl result is the matrix at the end of Figure 15. As noted above, changing this back to three equations gives us x=2, y=1, and z=1.