Figure 1
|
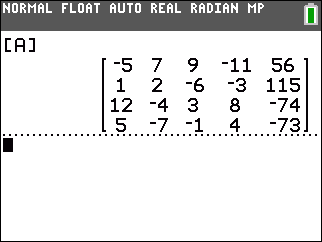
First we need to have the matrix defined in the calculator.
Earlier pages have demonstrated doing this.
Here we just verify, in Figure 1, that the matrix is
appropriately defined as [A].
|
Figure 2
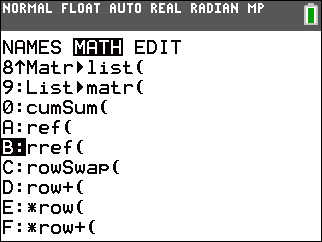 |
We find rref( in the MATH tab of the MATRIX window. Remember that we
get there via the   key sequence, followed
by using the key sequence, followed
by using the  key to move the highlight to the MATH tab. key to move the highlight to the MATH tab.
The we use the  key to move the selection highlight
down to the rref( option, as shown in Figure 2.
Once there, we can press the key to move the selection highlight
down to the rref( option, as shown in Figure 2.
Once there, we can press the  key to paste the function
name onto our main screen as is shown in Figure 3. key to paste the function
name onto our main screen as is shown in Figure 3.
|
Figure 3
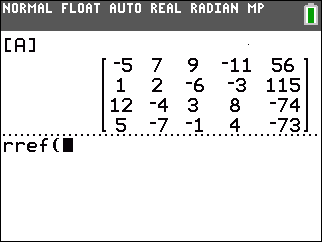 |
To complete the command we need to supply the name of the
matrix we are using. As we have seen in earlier pages, to input the
name of our matrix we need to return to the
MATRIX
window via the   keys. keys.
|
Figure 4
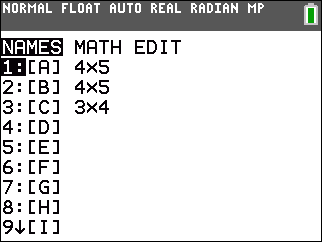 |
Figure 4 shows the MATRIX window on the calculator used for these
images. We know, from Figure 1, that the desired matrix is [A].
That is the currently selected matrix so we just need to
press the  key to paste that onto the main screen. key to paste that onto the main screen.
|
Figure 5
 |
Then we need to complete the command with a closing parenthesis,
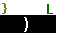 , as shown in Figure 6. , as shown in Figure 6.
|
Figure 6
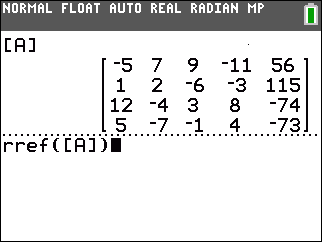 |
Once the command is formed, as it is here in Figure 6, we
just press  to get the calculator to
perform the function. to get the calculator to
perform the function.
|
Figure 7
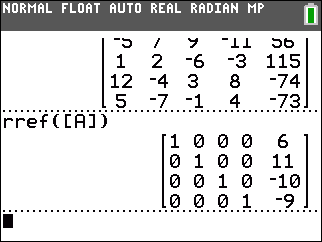 |
Figure 7 shows the result. That one statement,
rref([A]), did all of the work that we had to go through
in using the elementary row operations to generate the reduced row-echelon form
of the matrix. And, from this form we can read out the
solution,
x1 = 6,
x2 = 11,
x3 = –10,
and x4 = –9.
|


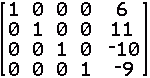



 key sequence, followed
by using the
key sequence, followed
by using the  key to move the highlight to the MATH tab.
key to move the highlight to the MATH tab.
 key to move the selection highlight
down to the rref( option, as shown in Figure 2.
Once there, we can press the
key to move the selection highlight
down to the rref( option, as shown in Figure 2.
Once there, we can press the  key to paste the function
name onto our main screen as is shown in Figure 3.
key to paste the function
name onto our main screen as is shown in Figure 3.


 keys.
keys.

 key to paste that onto the main screen.
key to paste that onto the main screen.

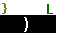 , as shown in Figure 6.
, as shown in Figure 6.

 to get the calculator to
perform the function.
to get the calculator to
perform the function.
