General NOTES for Math 169
Fifth Edition
Chapter 5

Introduction to Detailed Notes

This is a set of notes that have been made on reading the textbook. There is no real attempt to have comments on absolutely everything in the book noted here. At the same time, there is supplementary material here that is not in the book.

After writing out the notes for the first few sections, it has become clear that there is a tendency to make this a "teaching" document. As much as possible, efforts will be made to not do this. Rather, if there is teaching material to be presented then that will be done in separate pages, with pointers inserted here.

Chapter 5: Quadratic Equations & Inequalities

5.1 Quadratic Algebraic Expressions

All of the material in this section is a review of the work in chapter 4.

Page 279, at the bottom: the text recalls the use of the TABLE feature on the graphing calculator to check our work. First, we have done this before, back in Chapter 2, section 1. Second, there are web pages to step through the use of TABLEs on the TI-83, TABLEs on the TI-86, and TABLEs on the TI-89. Third, the TI-85 does not have a table feature. And, fourth, throughout this material we have been using an alternative method for checking ou work onthe calculator; namely, choose some strange value for the variable and then evaluate both the original expression and the equivalent answer expression.

Page 283, in information box #6: the suggestion here is to multiply the two binomials and then multiply that answer by the monomial. This order of multiplication is merely a suggestion. We would get the same result if we multiply the monomial times one of the binomials and then multiply that answer times the remaining binomial.

5.2 Quadratic Factoring Techniques

This is another review section.

Page 289, in information box #4: there is a suggestion that we should "memorize (or be able to generate) a list of the perfect squares". Certainly we can generate the squares with the graphing calculator. Memorizing the values would be nice, and it does come in handy, but it should not be a high priority.

In Example 4 on the same page, the explanation starts with "Possible factors are". There are many "possible factors", but the ones that are suggested in the text are the most reasonable guesses, and they would follow the pattern set by the difference of two squares.

Page 291, just above Example 2: the text "checks" the factoring by multiplying the factors, but it does it twice. This is not required. We know that multiplication is commutative, and that

(x+2)(x+4)=(x+4)(x+2) The book gives the two versions because it is not sure which way you would write the factorization. Once you have chosen the order of the factors, then a strict use of the FOIL method will produce one of the two versions given.

Page 295, information box 8: the discriminant, b²–4ac is introduced. We will come back to that expression. However, the statement "If b²–4ac=0, then the two linear binomial factors will be the same." is used in Example 2 in that information box.

Page 296, information box 9: we need to add a comment between Step 3 and Step 4 in the "Splitting the Middle Term" process. In particular, we need to say that if we can correctly split the middle term then the two binomial terms identified in Step 4 will always have a common binomial factor. In the example in the text, 6x² + 8x + 9x + 12 the first binomial 6x² + 8x and the second binomial 9x + 12 will have a common binomial factor. The "Splitting the Middle Term" process call for us to factor out the monomial 2x from the first binomial, yielding

2x(3x+4) At that point we know that we can factor a monomial from the second binomial, 9x+12, such that (3x+4) will be the other factor. In this case, that second binomial, 9x+12, factors to 3(3x+4). Now we are ready to move on to step 5.

5.3 Solving Quadratic Equations by Factoring

Having reviewed the techniques for factoring, this section move to solving quadratic equations by factoring and using the the multipliction property of zero. That proprety, and its use i solving quadratic equations by factoring is given at the top of page 301.

Page 304, after the solution to Example 2: the book suggest using the STORE feature on the graphing calculator to check the equation. I believe that the book means that if we use the graphing calculator, and if we store the approximate answer 2.646 into the variable x, then we can use the calculator to evaluate 3x²–21, and the result will be .003948. We can see this in the screen capture:

However, if we store the square root of 7 into x then the same expression evaluates to 0, as is shown in the screen capture:

Remember that the square root of 7 is NOT a rational number. It is irrational, and, therefore, it can not be represented by either a terminating or a repeating decimal. This figure above seems to indicate that the calculator is storing 2.645751311 as the approximation to the square root of 7. In fact, the calculator stores a few more digits to that approximation. It then uses that approximation in the computation of the value of the expression 3x²–21. The result is then rounded off to ten decimal places, producing the approximation 0 given above.

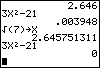
Just above Example 3, the text states

Note that 3x² 21 = 0 cannot be solved by factoring. This is not true. We could, however, correctly state that we can not solve the equation by factoring using integers, or even rational numbers. We know this by finding the value of the discriminant, in this case, 0² 4(3)(^–21) or 252 which is not a perfect square. According to section 5.2, information box 8, on page 295, this means that the expression cannot be factored using rational numbers.

Page 305, information box 6: note that the calculator image shows the TI-83 screen when it is in TRACE mode.

Page 305, at the bottom: note that the answers given for A6 are conveniently in Zdecimal mode, not Zstandard mode.

Page 307, bottom of information box #8: should refer to Section 5.4 (not 4.4).

5.4 Completing the Square, the Quadratic Formula & the Discriminant

Page 316: above and below the Example line: The quadratic formula is first given in two distinct parts:

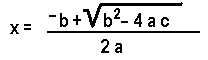
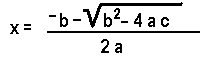
and then, below the Example line, it is given in its usual abbreviated form

Although the plus/minus sign was introduced earlier, it is important to remind students that the abbreviated version is just a short way to write the two longer versions at once.

Page 319, the Technology box: We have a slightly different version of this program or the TI-83, TI-85, and TI-86 calculators. Our version displays the value of the discriminant, and it gives the number of real number solutions along with the decimal value (at times, approximation) of those solutions. See the QUAD for the TI-83 page or the QUAD for the TI-85 and 86 page.

Page 320, top: It is important to realize that the screen captures presented at the top of the page are not from the program listed on the previous page. In fact, the book does not give us any idea of the source of that program, although it would be nice to find it.

Although we do not have the program used for the images at the top of page 320, we do have a similar program, called QUAD1. The QUAD1 web page describes that program, gives the appropiate listing and links to the various versions of the program, and gives examples of using the program.

5.5 Solving Quadratic Inequalities

Page 323, Technology box: Note that these images were generated on a TI-83 that was in Zstandard form, and was in Dot mode. Also, we should note that this ability to graph the inequality as

Y1=X²–5X–6<0 applies to the TI-83 and to the TI-85 and 86 (using the lowercase x). However, it does not work with the TI-89 and 92. For those calculators we nee to use the "tester()" function that was provided earlier.

Pages 329 and 330: Again, note that the calculator screen images show the screen in TRACE mode on a TI-83.

General NOTES for Math 169 Fifth EditionChapter 5