| To download, use the link QUAD. |

|
| To download, use the link QUAD. |

|
|
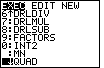
We start by pressing the
 key to obtain the menu of programs. Then we
use the
key to obtain the menu of programs. Then we
use the  key to move the highlight down to
the QUAD program, as shown in Figure 1. key to move the highlight down to
the QUAD program, as shown in Figure 1.
|

| We press the  key to leave Figure 1
and produce the bottom line of the screen on Figure 2. key to leave Figure 1
and produce the bottom line of the screen on Figure 2. |

|
We press the  key again to execute the QUAD
program. Figure 3 shows the immediate result. The program asks for a value for
the coefficient A.
Since we are looking at the problem key again to execute the QUAD
program. Figure 3 shows the immediate result. The program asks for a value for
the coefficient A.
Since we are looking at the problem
 key. This is the condition shown in Figure 3.
Then we press key. This is the condition shown in Figure 3.
Then we press  to have the calculator accept our answer.
This will move us to Figure 4. to have the calculator accept our answer.
This will move us to Figure 4.
|

| The calculator requests the value of B.
We respond with   .
The calculator asks for the value fo C.
We press the .
The calculator asks for the value fo C.
We press the  key. This produces the image seen in Figure 4. key. This produces the image seen in Figure 4. |

| We leave Figure 4 by pressing the  key.
The calculator processes the information given and produces the result seen
in Figure 5. In particular, we see that the value of the discriminant is 4,
that there are two answers, and that those values
are key.
The calculator processes the information given and produces the result seen
in Figure 5. In particular, we see that the value of the discriminant is 4,
that there are two answers, and that those values
are |
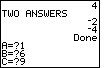
| Next we want to run the program to solve
 key.
Again the program requests the coeeficients, one at a time. We supply
those values to leave the screen as shown in Figure 6. key.
Again the program requests the coeeficients, one at a time. We supply
those values to leave the screen as shown in Figure 6.
|

| We leave Figure 6 by pressing the  key.
The calculator processes the information given and produces the result seen
in Figure 7. In particular, we see that the value of the discriminant is 0,
that there is one answers, and that answer is key.
The calculator processes the information given and produces the result seen
in Figure 7. In particular, we see that the value of the discriminant is 0,
that there is one answers, and that answer is |

| Next we want to run the program to solve
 key.
Again the program requests the coeeficients, one at a time. We supply
those values to leave the screen as shown in Figure 8. key.
Again the program requests the coeeficients, one at a time. We supply
those values to leave the screen as shown in Figure 8. |

| We leave Figure 8 by pressing the  key.
The calculator processes the information given and produces the result seen
in Figure 9. In particular, we see that the value of the discriminant is -4,
and that there are no Real Number answers. key.
The calculator processes the information given and produces the result seen
in Figure 9. In particular, we see that the value of the discriminant is -4,
and that there are no Real Number answers. |

| Next we want to run the program to solve
 key.
Again the program requests the coeeficients, one at a time. We supply
those values to leave the screen as shown in Figure 10. key.
Again the program requests the coeeficients, one at a time. We supply
those values to leave the screen as shown in Figure 10. |

| We leave Figure 10 by pressing the  key.
The calculator processes the information given and produces the result seen
in Figure 11. In particular, we see that the value of the discriminant is 8,
that there are two answers, and that those values are key.
The calculator processes the information given and produces the result seen
in Figure 11. In particular, we see that the value of the discriminant is 8,
that there are two answers, and that those values are
|
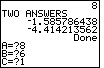
| Finally, we want to run the program to solve
 key.
Again the program requests the coeeficients, one at a time. We supply
those values to leave the screen as shown in Figure 12. key.
Again the program requests the coeeficients, one at a time. We supply
those values to leave the screen as shown in Figure 12. |

| We leave Figure 12 by pressing the  key.
The calculator processes the information given and produces the result seen
in Figure 13. In particular, we see that the value of the discriminant is 4,
that there are two answers, and that those values are key.
The calculator processes the information given and produces the result seen
in Figure 13. In particular, we see that the value of the discriminant is 4,
that there are two answers, and that those values are |
We noted in Figure 11 that when we have irrational answers, the QUAD program produces numeric approximations to those answers. A slightly enhanced version of the QUAD program is described in the quad1.htm page. That version produces the same values that are given by the QUAD program, but it also provides the more complete algebraic solution to the irrational answers.
©Roger M. Palay
Saline, MI 48176
August, 2010