Roadmap for Chapter 1

Proportions
Indirect		Direct
x*y = k		x/y = k
y = k/x		y = (1/k)*x
		y = m*x
Graph is a curve		Graph is a line through the origin
Example: x*y = 4		Example: x/y = 4
So: y = 4/x		So: y = (1/4)*x
In order to look at the curve or line just shown we needed to introduce the coordinate plane. This is a graph of the set of points that represent ordered pairs of values where the ordered pairs are understood to be of the form (x,y). In other words, the coordinate plane is the set {(x,y)| x and y are real numbers}.

		The coordinate plane
		Locate points
		Name the quadrants
		Midpoint between two points:
		Distance between two points:		Application of the Distance formula in the Battleship game Explaining the game Web versions of the game TI versions of the game
Function Notation: y = mx + b f(x) = mx + b f = {(x,y)| y = mx + b}		Slope-intercept form of the equation of a line. y = mx + b where m is the slope, and b is the second coordinate of the y-intercept
Inverse Notation: for the function f, the inverse of f is denoted as f -1 f -1( f(x) ) = x and f( f -1( x ) ) = x		Definitions of slope:
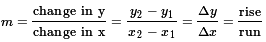
		Given an equation, graph the line
		Given the graph of a line, write the equation
		Horizontal lines
		Vertical lines
		Standard Form Ax + By = C, where A, B, and C are integers, (A is non-negative)
		Return to Vertical Lines
		Parallel Lines
		Perpendicular Lines
		Typical problems
		Approximating data that might be linear: Worked example TI-83/84 worked example I have more extensive web pages on linear regression and correlation coefficients for my Math 160 section. They are in Topic 8 at Topics in Statistics. I will create TI-84C versions of those pages as time permits.