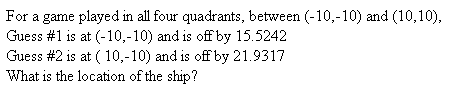Battleship Game

The Battleship Game presents a portion of the coordinate plane as an ocean. A battleship is supposedly located at one of the "lattice points" of that ocean, i.e., at a point with integer coordinates such as the point (4,7). The ship will not be at a point that does not have "nice" integer coordinates. When you play the game, either on the calculator or the web (see the main battleship page) you make guesses and the calaculator or web page tells you how far your guess is from the real ship location. For example, if the ship is at location (4,7), as shown in Figure 1 below, and you guess (9,4) then the distance from your guess to the ship is given as 5.8310.

Figure 1

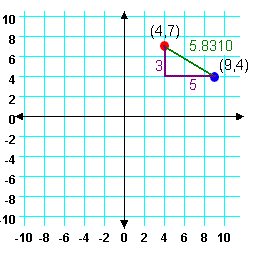
All that we know at that point is that the ship is a certain distance from our guess. We could identify all of the oints that are that distance from our guess. The circle in Figure 2 shows all of the points that are 5.8301 away from our guess at (9,4)

Figure 2

However, we actually know more than just the distance. For one thing, we know that the ship is within the area bounded by (0,0), (10,0), (10,10), and (0,10). Second we know that the ship is on "nice" integer points, "lattice points." Thus, when we guees a "nice" point such as (9,4), we are off some integer distance in the x values and some integer distance in the y values. Furthermore, we know that if we square the distance off in the x values and add that to the distance off in the y values we need to get the square of the distance from our guess to the ship. The square of 5.8310 (which is just an approximation of the distance) is 34.000561, which we then take as 34. Theerefore, we need to find the sum of two squares of integers that adds to 34. Here is a table of integers and their squares:

Table of squares
x

We see that the only two squares that we can add to get to a sum of 34 are 9 and 25. Therefore, our guess at (9,4) is off by 3 in one direction and 5 in the other. Which lattice points are off from (9,4) by 3 in one direction and 5 in the other? Points (6,9) [back 3 and up 5], (4,7) [back 5 and up 3], (4,1) [back 5 and down 3], and, although it is outside of our ocean, (6,-1) [back 3 and down 5]. There are four other points, way out of the ocean on the right side of the circle, (12,9), (14,7), (14,1), and (12,-1), but they are so far out that we just ignore them. Figure 3 shows the possible points.

Figure 3

We could try each of the three viable points as a second guess. In fact, if we were to guess (6,9) the calculator or web page would tell us that we are off by 2.828 units. Graphically, we could look at a circle with radius 2.828 and center at (6,9) to see just where we are. That is done in Figure 4.

Figure 4

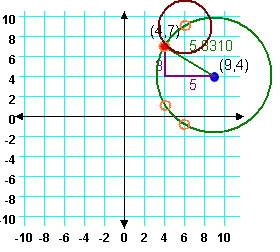It is clear from Figure 4 that the point (4,7) is the location of the ship. The interesting part is that we did not need to solve this graphically. Since we are off by 2.828, approximately, when we guess (6,9), we could look for two squares of integers whose sum is 2.828², or 8. Going back to our table, the only way to get the sum of two of the squared values to be 8 is to use 4 and 4. This corresponds to being off 2 in one direction and 2 in the other. Since our guess was at (6,9), the only possible values within the "ocean" would be (4,7) and (8,7). Of those two points, only (4,7) was viable from the first guess. Therefore, the battleship must be at (4,7).

Figure 5 presents the battleship problem when someone else has made two guesses, as is the case on the test question.

Figure 5

The first guess was at (0,0), the origin, and the second guess was at (10,0). The first guess misses the ship by 9.2195 units. We could draw the circle of points 9.2195 units from the origin to see all the points. But, we are looking for just the possible lattice points, the integer points. Again, wherever the ship is, it is on an integer point. Therefore the distance in the x direction and the distance in the y direction will be integers. The sum of the square of the distance off in the x direction plus the square of the distance off in the y direction must be equal to the square of 9.2195. The square of 9.2195 is 84.9991 or 85. Which pairs of values in the x² row in the table above will add to 85? In this case we have two such pairs, 4 and 81 is one pair and they correspond to being off by 2 in one direction and 9 in the other. The other pair is 36 and 49, corresponding to being off 6 in one direction and 7 in the other. Starting at the origin, (0,0), the points that are off by 2 and 9 from the first pair are (2,9) and (9,2). The points that are off by 6 and 7 from the second pair are (6,7) and (7,6). These points are circled in Figure 6.

Figure 6

Any of the four points would work, given just the first guess.

but, we have that second guess at (10,0) and it was off by 6.7028 and the square of that distance is 44.927 or 45. The only pair of squared values in the table that add to 45 is 9 and 36, corresponding to being off by 3 in one direction and 6 in the other. Off course, we are starting at our guess, (10,0), so the possible points are the ones that are back 3 and up 6 from our guess, or back 6 and up 3 from our guess. Those points are, respectively, (7,6) and (4,3). Of those, only (7,6) was in our list of possible points from the first guess. Therefore, the battleship must be at the point (7,6). [Actually, from just looking at Figure 6 and knowing the distance from our second guess, 6.7028, we could have eliminated all of the other points. (9.2) is way too close and (2,9) is way too far away. Even the point (6,7) has to be too far away since it is already 7 units away in the vertical direction. The leaves (7,6) as the only possible answer.]

A slightly more complex version of the game has an expanded ocean. Figure 7 gives the two guesses that actually determine the location of the ship.

Figure 7

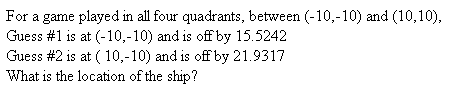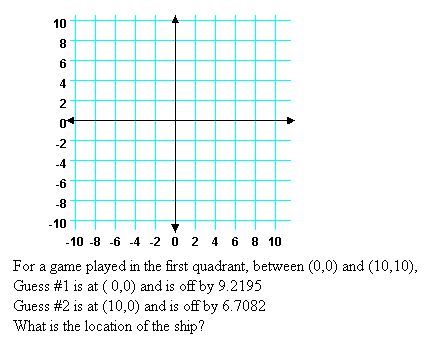
In this case the first guess was at (-10,-10) so we could be off by as much as 20 in both the vertical and horizontal directions. Therefore we will need to expand our table of squares:

Table of squares

Our first guess is off by 15.5242 and the square of that value, rounded off, is 241. The only pair of square values that add to 241 is 16 and 225, corresponding to being off by 4 and 15. The points that are 4 and 15 away from our guess at (-10,-10) are the ones that are over 4 and up 15, i.e., the point (-6,5), and the one that is over 15 and up 4, namely (5,-6). The second guess, at (10,-10) is off by 21.9317. Clearly, (5,-6) is too close. We can just check that the other point, (-6,5), works. It is off from our guess 16 units in the x direction and 15 units in the y direction. 16²+15² is 256+225 or 481. Our second guess guess was off by 21.9317 and 21.9317², rounded off, is 481. Therefore, the battleship is at the point (-6,5).