General NOTES for Math 169
Fifth Edition
Chapter 2

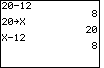Introduction to Detailed Notes

This is a set of notes that have been made on reading the textbook. There is no real attempt to have comments on absolutely everything in the book noted here. At the same time, there is supplementary material here that is not in the book.

After writing out the notes for the first few sections, it has become clear that there is a tendency to make this a "teaching" document. As much as possible, efforts will be made to not do this. Rather, if there is teaching material to be presented then that will be done in separate pages, with pointers inserted here.

Chapter 2: Linear Equations, Inequalities & Absolute Value

2.1 Solving Linear Equations - A Review

The material in this section is supposed to be a review, and it should be. I have no problem with the material as presented. However, in presenting the problems, the text places a small note at the end of each example showing the "CHECK" of the problem. We would do well to not only emphasize this check, but to point out that we can and should use the calculator to perform the CHECK. The problem at the bottom of page 76 is x-12=8 and the solution is x=20. The CHECK is to go back to the original problem and re-write it with the 20 replacing the x. On the calculator we can do this in four ways. First, we can write 20-12 and press the ENTER key to get the result. Second, we can store 20 into the variable X and then type X-12, press ENTER and get the result, 8. The following screen image shows both of these, either on the TI-83 or on the TI-85/86.

TI-83	TI-85 or TI-86

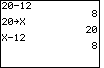A third and fourth methods employ the use of the relational operator, = on the TI-83 and on the TI-85/86, and the ability of the calculator to evaluate relational expressions. This will be new to most students, but we start using this idea in Section 2 without much of an introduction. When we form expressions with the relational operator, the result of that operation is 1 if the relation is true and 0 if it is false. Therefore, on the TI-83, if we enter 20-12=8, the calculator checks to see if this is a true statement, and, becuase it is true, the answer is 1. On the TI-85 (or TI-86), if we store 20 into the x variable and then enter x-128, the calculator determines that we have a true statement and it produces the value 1. If, on the TI-85 or 86 we enter x-126, then the calculator determines that we have a false statement and it returns the value 0. We can see this in the screen images below.

TI-83	TI-85 or TI-86

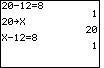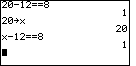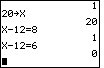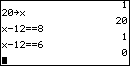NOTE: It is extremely important to use the double equal sign, , on the TI-85 and TI-86. These calculators will not give an error message if you use a single equal sign, but the result will not be what you expect.

The use of the TABLE feature of the TI calculators is a powerful aid in many areas of algebra. On pages 87-88 the text introduces this feature as way to check equivalent expressions. The pages ti83_tbl, ti86_tbl, and ti89_tbl give step-by-step presentations for using the TABLE feature of the TI-83, TI-86, and TI-89 calculators. There is no TABLE feature in the TI-85.

2.2 Solving Linear Inequalities

On page 95 the text introduces the concept of positive infinity, , and negative infinity, . We could also show the symbols and as general symbols for infinity, without regard to the sign.

The introduction of Interval Notation is both appropriate and helpful. However, we should include in here an apology with respect to using the same syntax for two different purposes. That is, the symbol (4,9) can mean either

the ordered pair (4,9), or
the open interval (4,9), i.e., the {x|4<x<9}

It is unfortunate that we use the same symbol for two different meanings, but that is the way it is. You need to understand the symbol in context in order to know which meaning is intended. Therefore, we could talk about the point (4,9), in which case we are talking about the ordered pair (4,9). On the other hand, we could talk about a point in (4,9), in which case we mean the interval (4,9), or the set of all points between 4 and 9.

The section on Technology on page 101 could use some further explanation and examples. This follows from the notes above with respect to "relational expressions". Where the earlier notes gave examples of the equality operators, either = on the TI-83 or on the TI-85/86, this section uses the operators, . These operators have two operands, that is they compare two values, one to the left and one to the right of the operator. Therefore, the expression 45 compares the two values 4 and 5. If the expression is true then it is assigned the value 1. If the expression is false, then it is assigned the value 0. The same is true for a more complex expression. In the book the calculator display in the middle of page 97 shows the expression 2X4. If X has the the value 1.3 then the left operand, 2X, has the value 2.6 which is NOT greater than or equal to 4. Therefore, the expression is false and it is assigned the value 0. If X has the value 3.9, then the left operand has the value 7.8 which is greater than 4. Therefore, in that case, the value of the expression is 1. The fact that when 2X4 is false we get the value 0 means that the graph of those false values is on the x-axis. When the value is true, the graph is elevated to the Y value of 1. It might be easier to see the graph if we enter the expression as (2X4)*3-1. The figures below demonstrate this new approach.

TI-83 Image TI-83 Description TI-86 Image TI-86 Description

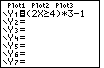On the TI-83 we move to the Y= screen and enter the desired expression. 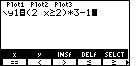On the TI-86 we move to the GRAPH screen, select the y(x)= menu option and enter the desired expression.

Before graphing the function, look at the MODE settings. Before graphing the function, we go back to the GRAPH menu, use the MORE key to find the FORMT option, and select that option to display this screen.

And, we move to the WINDOW screen to check and possibly change those settings. 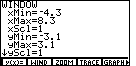And, we move back to the WINDOW (or RANGE on the TI-85) screen to check and possibly change those settings.

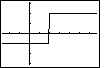Move to the GRAPH screen. Note the portion of the graph below the x-axis and the portion above the x-axis. Also note that the two portions are connected by an almost vertical line. The calculator does this because we had set the MODE for Connected. Move to the GRAPH screen. Note the portion of the graph below the x-axis and the portion above the x-axis. Also note that the two portions are connected by an almost vertical line. The calculator does this because we had set the FORMT for DrawLine.

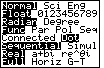We return to the MODE screen and select the Dot option. We return to the FORMT screen and select DrawDot.

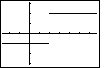Returning to the GRAPH screen, we get an unconnected graph. 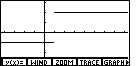Returning to the GRAPH screen, we get an unconnected graph.

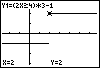Turn on the TRACE feature and position the marker to x=2. Note that the marker is at the top line. 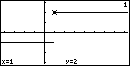Start the TRACE menu option and position the marker to x=2. Note that the marker is at the top line.

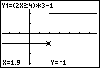Move back one position and the marker drops to the lower level. 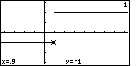Move back one position and the marker drops to the lower level.

Now, when the value of 2X4 is false, it becomes 0 and then 0*3-1 is just -1, and the graph is below the x-axis. And, when 2X4 is true, it becomes 1 and then 1*3-1 is 2, so the graph is elevated above the x-axis.

CAUTION: The text moves on to show that we can abbreviate an expression such as

-2<X and X<6 as a combined inequality in the form -2<X<6 However, the calculator does NOT evaluate this correctly. Instead, the calculator evaluates this expression by determining if 3<X is true or false. If it is false it is given the value 0 and if it is true it is given the value 1 . In either case, the resulting value is then compared to 6. Because both 0 and 1 are less than 6, this comparison always returns the value true, that is, the value 1. For the calculator we need to avoid the combined mode. However, the calculator does have both and and or operators. On the TI-83 these are found on the LOGIC portion of the TEST menu, as shown in the image below.

However, on the TI-86/85 these logical operators are found under the BASE menu, in the BOOL submenu, as shown in the image below.

Therefore, we can create an expression on the calculator that is exactly -2<X and X<6 Furthermore, we can modify that expression with the system shown above so that we can more easily see where the graph is above and below the x-axis. Thus, the expression becomes (-2<X and X<6)*3-1 The graphs of this for the TI-83 and TI-86 are given below:

TI-83		TI-86/85

2.3 Absolute Value

The material in the text on absolute valeus seems quite well organized and complete. However, I would like students to consider the alternative approach given on my absolute value page. With respect to using the calculators, we should demonstrate a problem or two on both the TI-83 and the TI-86. How about Q16d on page 121. The problem is to solve

|6x+8|+26 See ti83_abs for the TI-83 screens and and ti86_abs for the TI-86/85 screens.