There are two ways to
enter a matrix into the calculator. First, you can use the [ and ] characters to type
the matrix directly into the calcualtor. That method was demonstrated in
the 3 variable, 3 equation page.
Second, you can use the Matrix Editor. That is the method presented here, in Figures 1 through 6.
The other Figures on this page are used to demonstrate
how the calculator produces the reduced row echelon form of the given matrix.
Figure 1
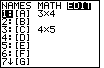
| Open the matrix menu with the  key.
Use key.
Use   to move the highlight
to the EDIT command at the top of the screen.
The calculator used here has two previously defined matrices, [A] and [C].
For this problem we will re-use matrix [A].Note that matrix [A] is already selected.
Therefore, press to move the highlight
to the EDIT command at the top of the screen.
The calculator used here has two previously defined matrices, [A] and [C].
For this problem we will re-use matrix [A].Note that matrix [A] is already selected.
Therefore, press  to move to Figure 2. to move to Figure 2.
|
Figure 2
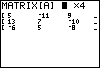
| Before we edit the numbers that are in the matix, the calculator allows us
to change the size of the matrix. [A] has 3 rows and 4 columns from its earlier definition.
We need to make [A] have seven rows and eight columns. Therefore,
press  
  to make this change and move to Figure 3. to make this change and move to Figure 3.
|
Figure 3

| Notice in Figure 3 that the matrix [A] appears in its expanded form.
By default, the
new cells of the matrix have been assigned the value 0.
The highlight is on the item at row 1 column 1. The old value for that cell was 5, as shown here in the
matrix and in Figure 2. The new value will be 2. We have pressed the
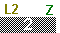 key to enter that new value. It appears at the bottom of the
screen. To get the calculator to accept that value, press key to enter that new value. It appears at the bottom of the
screen. To get the calculator to accept that value, press
 . .
|
Figure 4
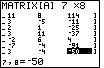
| Figure 4 shows the rightmost 3 columns of elements in the matrix after all 56 values
have been entered.
|
Figure 5

| Use the  key to move the highlight to the left
in order to shift the display so that we can see other columns.
The highlight in Figure 5 is on the item in row 7 column 3. Thus, the screen in Figure 5
displays columns 3, 4, and 5. key to move the highlight to the left
in order to shift the display so that we can see other columns.
The highlight in Figure 5 is on the item in row 7 column 3. Thus, the screen in Figure 5
displays columns 3, 4, and 5.
|
Figure 6

| Use the  key to move the highlight to the left
in order to shift the display so that we can see remaining columns.
The highlight in Figure 6 is on the item in row 7 column 1. Thus, the screen in Figure 6
displays columns 1, 2, and 3. key to move the highlight to the left
in order to shift the display so that we can see remaining columns.
The highlight in Figure 6 is on the item in row 7 column 1. Thus, the screen in Figure 6
displays columns 1, 2, and 3.
After we have verified the contents of [A], we exit the
matrix editor via the   key sequence. This will return the calculator to the main screen.
key sequence. This will return the calculator to the main screen.
|
Figure 7
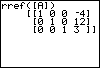
| The main screen of the calculator used here still shaows the previous command
used, rref([A]), and the results of that command. In fact, that was the
command used in the previous example page,
s3_3x3o.htm. Since then we have changed the size and the contents
of [A]. Nonetheless, we want to construct that same command. We can do that
by recalling the last command by pressing
  . The result is shown in Figure 8. . The result is shown in Figure 8.
|
Figure 8
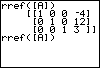
| The command has been recalled. Press
 to perform the command. to perform the command.
|
Figure 9
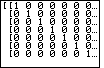
| THe reduced row echelon form of the matrix appears in Figure 9.
Unfortunately, we can only see the leftmost 7 columns. They have the expected 1's
down the main diagonal with 0's above and below.
The final column is off the screen. However, we can use the
 key to shift the display to the right. key to shift the display to the right.
|
Figure 10

| Now we can see the eighth column. We could translate this matrix
back to the equation format to produce:
1s + 0t + 0u + 0v + 0w + 0x + 0y = 5
0s + 1t + 0u + 0v + 0w + 0x + 0y = -7
0s + 0t + 1u + 0v + 0w + 0x + 0y = 8
0s + 0t + 0u + 1v + 0w + 0x + 0y = -6
0s + 0t + 0u + 0v + 1w + 0x + 0y = -9
0s + 0t + 0u + 0v + 0w + 1x + 0y = 2
0s + 0t + 0u + 0v + 0w + 0x + 1y = -3
which simplifies to s=5, t=–7, u=8, v=– 6, w=– 9,
x=2, and y=– 3.
|
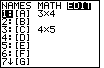
 key.
Use
key.
Use 
 to move the highlight
to the EDIT command at the top of the screen.
The calculator used here has two previously defined matrices, [A] and [C].
For this problem we will re-use matrix [A].Note that matrix [A] is already selected.
Therefore, press
to move the highlight
to the EDIT command at the top of the screen.
The calculator used here has two previously defined matrices, [A] and [C].
For this problem we will re-use matrix [A].Note that matrix [A] is already selected.
Therefore, press  to move to Figure 2.
to move to Figure 2.
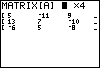

 to make this change and move to Figure 3.
to make this change and move to Figure 3.

 key to enter that new value. It appears at the bottom of the
screen. To get the calculator to accept that value, press
key to enter that new value. It appears at the bottom of the
screen. To get the calculator to accept that value, press
 .
.
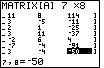

 key to move the highlight to the left
in order to shift the display so that we can see other columns.
The highlight in Figure 5 is on the item in row 7 column 3. Thus, the screen in Figure 5
displays columns 3, 4, and 5.
key to move the highlight to the left
in order to shift the display so that we can see other columns.
The highlight in Figure 5 is on the item in row 7 column 3. Thus, the screen in Figure 5
displays columns 3, 4, and 5.

 key to move the highlight to the left
in order to shift the display so that we can see remaining columns.
The highlight in Figure 6 is on the item in row 7 column 1. Thus, the screen in Figure 6
displays columns 1, 2, and 3.
key to move the highlight to the left
in order to shift the display so that we can see remaining columns.
The highlight in Figure 6 is on the item in row 7 column 1. Thus, the screen in Figure 6
displays columns 1, 2, and 3.

 key sequence. This will return the calculator to the main screen.
key sequence. This will return the calculator to the main screen.
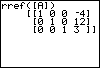

 . The result is shown in Figure 8.
. The result is shown in Figure 8.

 to perform the command.
to perform the command.
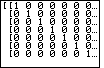
 key to shift the display to the right.
key to shift the display to the right.

 key.
The text below will be done from the perspective of the TI-83. That is, all
reference to the MATRIX key will be demonstrated via the
key.
The text below will be done from the perspective of the TI-83. That is, all
reference to the MATRIX key will be demonstrated via the
 .
In addition, the
.
In addition, the  and the
and the  , again to save space.
, again to save space.