TI-83: Simple 3 equation 3 variable, missing values
The main page for solving systems of linear equations on the TI-83 and TI-83 Plus.
The previous example page covers a Simple 7 equation 7 variable situation.
The next example page covers a Simple 4 equation 4 variable situation,
but with both missing terms and other variables.
WARNING: The TI-83 and TI-83 Plus are almost identical in terms of the material presented here.
The major difference is the labels that are on certain keys. The TI-83
has a  key, whereas on the TI-83 Plus
requires 2 keys to achieve the same result, namely, the
key, whereas on the TI-83 Plus
requires 2 keys to achieve the same result, namely, the

 key.
The text below will be done from the perspective of the TI-83. That is, all
reference to the MATRIX key will be demonstrated via the
key.
The text below will be done from the perspective of the TI-83. That is, all
reference to the MATRIX key will be demonstrated via the
 key. If the user has a TI-83 Plus then the key strokes should be
key. If the user has a TI-83 Plus then the key strokes should be

 .
To save some space, and to ignore this difference, the numeric keys
(the gray ones) have been changed in some places to show the key
face, as in
.
To save some space, and to ignore this difference, the numeric keys
(the gray ones) have been changed in some places to show the key
face, as in  .
In addition, the
.
In addition, the  key may be shown as
key may be shown as  and the
and the  key may be shown as
key may be shown as  , again to save space.
, again to save space.
The problem we will use on this page is
4x + 7y = 48
3x - 8y + 4z = -50
-5y + 11z = 15
Our first step is to identify the variables. In this case, the
variables are x, y, and z,
although the first equation does not have a z
and the third equation is missing an x term.
Second we need to decide on the order of the varaibles, and the traditional x,
then y, then z
seems reasonable. Third, we can rewrite the equations, with the variables in order, and
not leaving any out. We will add a z term to the first, but with a coefficient of 0.
We will add an x term to the third equation, again with a coefficent of 0. The
rewrite of the problem produces
4x + 7y + 0z= 48
3x - 8y + 4z = -50
0x - 5y + 11z = 15
By adding the extra terms (having 0 as the coefficient) we have not changed any equation
but we have changed the form of the equation so that it fits the same pattern that we
have been using in the earlier pages. We are ready to use the calculator.
Figure 1
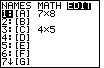
| To get the calculator to Figure 1, press
 to open the MATRIX menu, and to open the MATRIX menu, and
  to shift the display to the EDIT submenu. The calcualtor used here has two previously defined
matrices, [A] with 7 rows and 8 columns, and [C] with 4 rows and 5 columns. We need
to have a 3 row and 4 column matrix. Matrix [A] is highlighted.
Press
to shift the display to the EDIT submenu. The calcualtor used here has two previously defined
matrices, [A] with 7 rows and 8 columns, and [C] with 4 rows and 5 columns. We need
to have a 3 row and 4 column matrix. Matrix [A] is highlighted.
Press  to move to Figure 2 where we can change the size of
[A] and then change its contents. to move to Figure 2 where we can change the size of
[A] and then change its contents.
|
Figure 2

| Figure 2 shows the status of [A] before we make any changes.
We change the size of the matrix by pressing
 
  to produce the 3 rows and 4 columns shown in
Figure 3. to produce the 3 rows and 4 columns shown in
Figure 3.
|
Figure 3
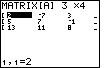
| The size of [A] has changed, now we need to change the contents of the matrix to
reflect the three equations that we have.
4x + 7y + 0z= 48
3x - 8y + 4z = -50
0x - 5y + 11z = 15
For such equations, we want then matrix to hold
| 4 | 7 | 0 | 48 |
| 3 | – 8 | 4 | – 50 |
| 0 | – 5 | 11 | 15 |
|
Figure 4
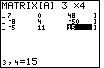
| Figure 4 shows the calculator display after all of the new values have been entered.
Note that we can seen the final 3 columns of entries.
|
Figure 5
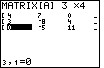
| Use the  key to move the highlight to the left
until it is at the first row. Now the display shows the rest of the matrix.
Once we have confirmed that the matrix holds thedesired values,
we can leave the matrix editor by pressing the key to move the highlight to the left
until it is at the first row. Now the display shows the rest of the matrix.
Once we have confirmed that the matrix holds thedesired values,
we can leave the matrix editor by pressing the
  key sequence.
That will return us to the main screen. key sequence.
That will return us to the main screen.
|
Figure 6

| The calculator used here had been used to solve the
problem presented on the previous page.
Therefore, the main calculator page holds the solution matrix from that page.
We need to construct the rref([A]) command on this main calculator page.
|
Figure 7

| To construct the rref[A]) command we use the
 key to open the MATRIX menu,
and then the key to open the MATRIX menu,
and then the  key to move to the MATH
sub-menu, shown in Figure 8. key to move to the MATH
sub-menu, shown in Figure 8.
|
Figure 8

| Once on the MATH sub-menu, use the  key to move the highlight down until it points to the
rref( command. Then, press
key to move the highlight down until it points to the
rref( command. Then, press  to paste that
command onto the main calculator page. to paste that
command onto the main calculator page.
|
Figure 9

| We complete the command in Figure 9 by pressing
 to return to the MATRIX menu. The NAMES sub-menu will
be displayed and the [A] matrix will be highlighted. Press to return to the MATRIX menu. The NAMES sub-menu will
be displayed and the [A] matrix will be highlighted. Press  to paste the highlighted value, [A], onto the main page. Add the final parentheis
to the command with the
to paste the highlighted value, [A], onto the main page. Add the final parentheis
to the command with the  key. key.
|
Figure 10

| Press  to have the calculator perform the command. The result is
shown in Figure 10. This is a matrix representation for the
equations
1x + 0y + 0z= – 2 to have the calculator perform the command. The result is
shown in Figure 10. This is a matrix representation for the
equations
1x + 0y + 0z= – 2
0x + 1y + 0z = 8
0x + 0y + 1z = 5
Which means that the solution is x=– 2, y=8, and z=5.
|
The main page for solving systems of linear equations on the TI-83 and TI-83 Plus.
The previous example page covers a Simple 7 equation 7 variable situation.
The next example page covers a Simple 4 equation 4 variable situation,
but with both missing terms and other variables.
©Roger M. Palay
Saline, MI 48176
November, 2010
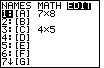
 to open the MATRIX menu, and
to open the MATRIX menu, and

 to shift the display to the EDIT submenu. The calcualtor used here has two previously defined
matrices, [A] with 7 rows and 8 columns, and [C] with 4 rows and 5 columns. We need
to have a 3 row and 4 column matrix. Matrix [A] is highlighted.
Press
to shift the display to the EDIT submenu. The calcualtor used here has two previously defined
matrices, [A] with 7 rows and 8 columns, and [C] with 4 rows and 5 columns. We need
to have a 3 row and 4 column matrix. Matrix [A] is highlighted.
Press  to move to Figure 2 where we can change the size of
[A] and then change its contents.
to move to Figure 2 where we can change the size of
[A] and then change its contents.




 to produce the 3 rows and 4 columns shown in
Figure 3.
to produce the 3 rows and 4 columns shown in
Figure 3.
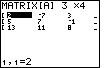

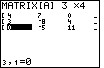
 key to move the highlight to the left
until it is at the first row. Now the display shows the rest of the matrix.
Once we have confirmed that the matrix holds thedesired values,
we can leave the matrix editor by pressing the
key to move the highlight to the left
until it is at the first row. Now the display shows the rest of the matrix.
Once we have confirmed that the matrix holds thedesired values,
we can leave the matrix editor by pressing the

 key sequence.
That will return us to the main screen.
key sequence.
That will return us to the main screen.


 key to open the MATRIX menu,
and then the
key to open the MATRIX menu,
and then the  key to move to the MATH
sub-menu, shown in Figure 8.
key to move to the MATH
sub-menu, shown in Figure 8.

 key to move the highlight down until it points to the
rref( command. Then, press
key to move the highlight down until it points to the
rref( command. Then, press  to paste that
command onto the main calculator page.
to paste that
command onto the main calculator page.

 to return to the MATRIX menu. The NAMES sub-menu will
be displayed and the [A] matrix will be highlighted. Press
to return to the MATRIX menu. The NAMES sub-menu will
be displayed and the [A] matrix will be highlighted. Press  to paste the highlighted value, [A], onto the main page. Add the final parentheis
to the command with the
to paste the highlighted value, [A], onto the main page. Add the final parentheis
to the command with the 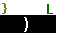 key.
key.

 to have the calculator perform the command. The result is
shown in Figure 10. This is a matrix representation for the
equations
to have the calculator perform the command. The result is
shown in Figure 10. This is a matrix representation for the
equations  key.
The text below will be done from the perspective of the TI-83. That is, all
reference to the MATRIX key will be demonstrated via the
key.
The text below will be done from the perspective of the TI-83. That is, all
reference to the MATRIX key will be demonstrated via the
 .
In addition, the
.
In addition, the  and the
and the  , again to save space.
, again to save space.