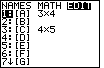
 key and
then shift the highlight to the right with the
key and
then shift the highlight to the right with the

 keys.
The calculator used here has two previously defined matrices, [A] and [C].
For this problem we will re-use matrix [A]. Because [A] is already highlighted, press
keys.
The calculator used here has two previously defined matrices, [A] and [C].
For this problem we will re-use matrix [A]. Because [A] is already highlighted, press
 to select that matrix.
to select that matrix.




 to produce Figure 2.
Note that the calculator has added the fourth row and that all of the valeus in that row have
been set to 0.
to produce Figure 2.
Note that the calculator has added the fourth row and that all of the valeus in that row have
been set to 0.
Now we need to enter each of the values from the matrix given above.
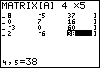

 key to shift the display to show the first columns of the matrix.
Now we can verify the contents of those columns.
key to shift the display to show the first columns of the matrix.
Now we can verify the contents of those columns.


 to return to the main screen, shown in Figure 5.
This screen shows the results that were left on the calculator from a previous
example. Fortunately, teh previous command is exactly the one that we want
to issue again, but this time the command will use our revised matrix [A].
to return to the main screen, shown in Figure 5.
This screen shows the results that were left on the calculator from a previous
example. Fortunately, teh previous command is exactly the one that we want
to issue again, but this time the command will use our revised matrix [A].
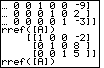

 to recall the previous command.
to recall the previous command.
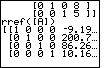
 to execute the command. The result is
shown in Figure 7. The values for the variables appear in the final column.
It is possible that these are the correct valeus, but we do not expect to get
fractional answers. All of the previous examples have produced nice integer answers.
Perhaps there was an error in our original matrix.
Fortunately, the orginal matrix is still there in [A].
to execute the command. The result is
shown in Figure 7. The values for the variables appear in the final column.
It is possible that these are the correct valeus, but we do not expect to get
fractional answers. All of the previous examples have produced nice integer answers.
Perhaps there was an error in our original matrix.
Fortunately, the orginal matrix is still there in [A].
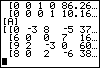
 key, and we select the name of our matrix, [A],
by pressing the
key, and we select the name of our matrix, [A],
by pressing the  key. This will paste the name of the matrix onto the main
screen, as shown in Figure 8. Then press the
key. This will paste the name of the matrix onto the main
screen, as shown in Figure 8. Then press the  to display the va;ue of the matrix.
to display the va;ue of the matrix.
A comparison between the matrix shown in Figure 8 and the matrix
| 0 | – 3 | 8 | – 5 | – 37 |
| 6 | 30 | 0 | 7 | 16 |
| 9 | 2 | – 3 | 0 | 60 |
| 8 | 0 | 2 | – 6 | 38 |
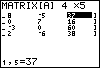
 to open the matrix menu,
to open the matrix menu, 
 to select the matrix editor,
to select the matrix editor,  to edit [A], and then
use the
to edit [A], and then
use the  key to move the highlight to the item at
row 1 coumn 5.
key to move the highlight to the item at
row 1 coumn 5.
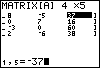


 . Note that the new value is shown at the bottom
of the screen. The new value will not be placed into the matrix
until we press the
. Note that the new value is shown at the bottom
of the screen. The new value will not be placed into the matrix
until we press the  key, which will move us to Figure 11.
key, which will move us to Figure 11.
 key a few times to shift the display to
show the final column. This was done to produce Figure 12.
key a few times to shift the display to
show the final column. This was done to produce Figure 12.



 to return to the main screen, then press
to return to the main screen, then press 
 to recall the [A] command, and press
to recall the [A] command, and press 
 to recall the rref[A] command. The result is shown in Figure 13.
to recall the rref[A] command. The result is shown in Figure 13.
Finally, press press  to perform the rref[A] command.
to perform the rref[A] command.

 key.
The text below will be done from the perspective of the TI-83. That is, all
reference to the MATRIX key will be demonstrated via the
key.
The text below will be done from the perspective of the TI-83. That is, all
reference to the MATRIX key will be demonstrated via the
 .
In addition, the
.
In addition, the  , again to save space.
, again to save space.