TI-83: Simple 2 equation 2 variable, parallel lines

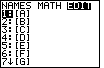
Figure 1	Open the matrix menu with the key and then shift the highlight to the right with the keys. The calculator used here has no previously defined matrices. For this problem we will use matrix [A]. Because [A] is already highlighted, press to select that matrix.
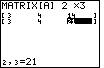
Figure 2	In order to size and fill the matrix, press to specify 2 rows and to specify 3 columns. Then fill the matrix with the desired values: . The result should be identical to that shown in Figure 2.
Figure 3	Exit the matrix editor and return to the main screen by pressing . This particular calculator has a clear main screen. We want to create the command rref([A]).
Figure 4	To do this we return to the matrix menu via the key, and we move to the MATH menu via the key. Then, use the key to move the highlight down the list of options until the highlight is on the rref( item, as shown in Figure 4.
Figure 5	To move from Figure 4 to Figure 5, press the key to select the highlighted option and paste it onto the main screen.
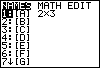
Figure 6	In order to complete the command we need to produce the name of the matrix, [A]. We return to the matrix menu via the key. This brings up the matrix menu, and opens the NAMES sub-menu. In fact, our desired matrix, [A], is already highlighted. Therefore, press to paste the name onto the main screen, shown in Figure 7.
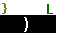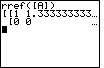
Figure 7	In Figure 7 we have completed the command by pressing , and we have instructed the calculator to perform the command by pressing the key. The result is shown in Figure 7. Even though we can not see the entire matrix in Figure 7, we4 can see enough to tell us that we have a problem here. In all of the previous examples, the reduced row echelon form of the matrix has had 1's down the main diagonal and 0's above and below those 1's. The matrix in Figure 7 does not look like that at all. The first row starts with a 1 but that is folloed by the decimal version of 4/3. The second row starts with two 0's. We do not have a diagonal of 1's! We will use the key to move the display to show the third and final column.
Figure 8	Now that we can see the third column, we could construct the entire resulting reduced row echelon matrix: 1 4/3 0 0 0 1 This matrix represents the system of equations: 1x + (4/3)y = 0 0x + 0y = 1 Although the first of these equations is possible, the second can not have any solution. No matter what values we choose for x and y, if we multiply them by 0 the products will be 0, and the sum of the two 0's will be 0, not 1. Therefore, this matrix indicates that there is no solution to the original system of linear equations.

If we return to the original problem,

The main page for solving systems of linear equations on the TI-85 and TI-86.
The previous example page covers a Simple 4 equation 4 variable situation but with missing and other varaibles.
The next example page covers a Simple 3 equation 3 variable situation, but with no solution since two planes are parallel.