Figure 1

| Open the matrix menu with the  key and
then shift the highlight to the right with the key and
then shift the highlight to the right with the
  keys.
The calculator used here has one previously defined matrix, namely, [A].
For this problem we will re-use matrix [A]. Because [A] is already highlighted, press keys.
The calculator used here has one previously defined matrix, namely, [A].
For this problem we will re-use matrix [A]. Because [A] is already highlighted, press
 to select that matrix. to select that matrix.
|
Figure 2

| The existing [A] has two rows and three columns. We want
the matrix to hold three rows and four columns. Before we place new values into the matrix, the editor allows us to
change the size of the matrix.
|
Figure 3

| In order to size and fill the matrix, press   to specify
3 rows and to specify
3 rows and   to specify 4 columns.
Then fill the matrix with the desired values: to specify 4 columns.
Then fill the matrix with the desired values:
 
  
 
    
 
 
  
  
  
   
  
    .
The result should be
identical to that shown in Figure 3. The final three columns of the
matrix are visible in Figure 3. We can verify the values in those three columns. .
The result should be
identical to that shown in Figure 3. The final three columns of the
matrix are visible in Figure 3. We can verify the values in those three columns.
|
Figure 4
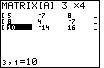
| We use the  key to move the highlight back to the first column so
that we can verify the values in that column. key to move the highlight back to the first column so
that we can verify the values in that column.
|
Figure 5

| Leave the matrix editor by pressing   .
This returns us to the main screen.
For the calculator used here, the main screen shows us the results from
the computation of the previous example. In particular, the previous command,
rref([A]), is exactly the command that we want to give again. .
This returns us to the main screen.
For the calculator used here, the main screen shows us the results from
the computation of the previous example. In particular, the previous command,
rref([A]), is exactly the command that we want to give again.
|
Figure 6

| Recall the previous command by pressing the
keys   . This produces the image shown in Figure 6.
We could tell the calculator to perform the command, but we will take this opportunity to add the
"change it to a fraction" command to the end of the current command. We will do this so that the
eventual resulting matrix will display fractions instead of decimal approximation. . This produces the image shown in Figure 6.
We could tell the calculator to perform the command, but we will take this opportunity to add the
"change it to a fraction" command to the end of the current command. We will do this so that the
eventual resulting matrix will display fractions instead of decimal approximation.
|
Figure 7
| Use the  key to open the MATH menu which is shown in Figure 7.
Then, we can select the "change it to a fraction" command by pressing key to open the MATH menu which is shown in Figure 7.
Then, we can select the "change it to a fraction" command by pressing  . .
|
Figure 8

| The top three lines in Figure 8 are left over from an earlier example. THe fourth line in Figure 8 contains
the command that we recalled and modified. To execute this new command we press  .
The result is the matrix shown in lines 5 through 7 of the display.
Again, as was the case in the previous example, this is is not the matrix that we expect to find.
We expect to have 1's down the main diagonal with 0's above and below that diagonal.
Instead, the third row, third column position holds a 0, and both the third column first and second
rows do not hold 0's. If we translate the matrix back into a system of equations we get .
The result is the matrix shown in lines 5 through 7 of the display.
Again, as was the case in the previous example, this is is not the matrix that we expect to find.
We expect to have 1's down the main diagonal with 0's above and below that diagonal.
Instead, the third row, third column position holds a 0, and both the third column first and second
rows do not hold 0's. If we translate the matrix back into a system of equations we get
| 1x + 0y – (17/76)z | = 0 |
| 0x + 1y – (-99/76)z | = 0 |
| 0x + 0y + 0z | = 1 |
Although the first and second of these equations are possible, the third can not have any solution.
No matter what values we choose for x, y, and z, if we multiply them by 0
the products will be 0, and the sum of the three 0's will be 0, not 1.
Therefore, this matrix indicates that there is no solution to the original system of linear equations.
|

 key and
then shift the highlight to the right with the
key and
then shift the highlight to the right with the

 keys.
The calculator used here has one previously defined matrix, namely, [A].
For this problem we will re-use matrix [A]. Because [A] is already highlighted, press
keys.
The calculator used here has one previously defined matrix, namely, [A].
For this problem we will re-use matrix [A]. Because [A] is already highlighted, press
 to select that matrix.
to select that matrix.



 to specify
3 rows and
to specify
3 rows and 
 to specify 4 columns.
Then fill the matrix with the desired values:
to specify 4 columns.
Then fill the matrix with the desired values:



































 .
The result should be
identical to that shown in Figure 3. The final three columns of the
matrix are visible in Figure 3. We can verify the values in those three columns.
.
The result should be
identical to that shown in Figure 3. The final three columns of the
matrix are visible in Figure 3. We can verify the values in those three columns.
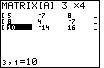
 key to move the highlight back to the first column so
that we can verify the values in that column.
key to move the highlight back to the first column so
that we can verify the values in that column.


 .
This returns us to the main screen.
For the calculator used here, the main screen shows us the results from
the computation of the previous example. In particular, the previous command,
rref([A]), is exactly the command that we want to give again.
.
This returns us to the main screen.
For the calculator used here, the main screen shows us the results from
the computation of the previous example. In particular, the previous command,
rref([A]), is exactly the command that we want to give again.


 . This produces the image shown in Figure 6.
We could tell the calculator to perform the command, but we will take this opportunity to add the
"change it to a fraction" command to the end of the current command. We will do this so that the
eventual resulting matrix will display fractions instead of decimal approximation.
. This produces the image shown in Figure 6.
We could tell the calculator to perform the command, but we will take this opportunity to add the
"change it to a fraction" command to the end of the current command. We will do this so that the
eventual resulting matrix will display fractions instead of decimal approximation.

 key to open the MATH menu which is shown in Figure 7.
Then, we can select the "change it to a fraction" command by pressing
key to open the MATH menu which is shown in Figure 7.
Then, we can select the "change it to a fraction" command by pressing  .
.

 .
The result is the matrix shown in lines 5 through 7 of the display.
Again, as was the case in the previous example, this is is not the matrix that we expect to find.
We expect to have 1's down the main diagonal with 0's above and below that diagonal.
Instead, the third row, third column position holds a 0, and both the third column first and second
rows do not hold 0's. If we translate the matrix back into a system of equations we get
.
The result is the matrix shown in lines 5 through 7 of the display.
Again, as was the case in the previous example, this is is not the matrix that we expect to find.
We expect to have 1's down the main diagonal with 0's above and below that diagonal.
Instead, the third row, third column position holds a 0, and both the third column first and second
rows do not hold 0's. If we translate the matrix back into a system of equations we get
 key.
The text below will be done from the perspective of the TI-83. That is, all
reference to the MATRIX key will be demonstrated via the
key.
The text below will be done from the perspective of the TI-83. That is, all
reference to the MATRIX key will be demonstrated via the
 , again to save space.
, again to save space.