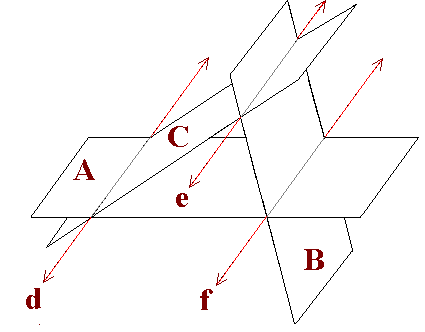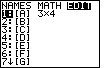
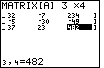
Verify the values.


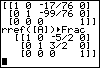
 to have the calculator perform the command. The result is the matrix shown
at the bottom of the screen.
to have the calculator perform the command. The result is the matrix shown
at the bottom of the screen.
As was the case in the previous example, the resulting matrix does not have the diagonal 1's form. And, in the same way that we looked at the previous example, it is clear that there is no possible solution to the matrix given in Figure 5. Therefore, this matrix indicates that there is no solution to the original system of linear equations.
 key, whereas on the TI-83 Plus
requires 2 keys to achieve the same result, namely, the
key, whereas on the TI-83 Plus
requires 2 keys to achieve the same result, namely, the

 key.
The text below will be done from the perspective of the TI-83. That is, all
reference to the MATRIX key will be demonstrated via the
key.
The text below will be done from the perspective of the TI-83. That is, all
reference to the MATRIX key will be demonstrated via the
 .
In addition, the
.
In addition, the  key may be shown as
key may be shown as  , again to save space.
, again to save space.