Chapter 11: Vectors and the Geometry of Space

1. Section 11.1: Vectors in the Plane
   • Vectors have magnitude and direction, but no location.
   • An instance of a vector might be described as the directed line segment form an initial point, say (3,4), to a terminal point, say (8,16). However, this vector is equivalent to any vector that goes from an inital point (a,b) to a terminal point (a+5,b+12).
   • find magnitude of the vector from `P=(x_1,y_1)` to `Q=(x_2,y_2)`. This is just the distance between the points so the magnitude of `||vec(PQ)||=sqrt((x_2-x_1)^2+(y_2-y_1)^2)`.
   • find component form, this is the instance of the vector with the initial point at the origin. Thus, our vector from `P=(x_1,y_1)` to `Q=(x_2,y_2)`, namely, `vec(PQ)`, would be the vector from `(0,0)` to `(x_2-x_1,y_2-y_1)` and in that case we could write the vector in the form `bb v = \ltx_2-x_1,y_2-y_1\gt` and we call `x_2-x_1` and `y_2-y_1` components.
   • (a,b) vs. <a,b>
   • add vectors
   • muliply by a scalar
   • zero vector: 0 vs. 0
   • length of scalar multiple of vector
   • unit vector in same direction, given `bbv=\ltx_1,y_1\gt` the unit vector in the same direction as `bbv` will be `\ltx_1/(||bbv||),y_1/(||bbv||)\gt` where `||bbv||=sqrt(x_1^2+y_1^2)`.
   • standard unit vectors `bbi=\lt1,0\gt` and `bbj=\lt0,1\gt`
   • linear combinations of `bbi` and `bbj`
   • vector subtraction
2. Section 11.2: Space Coordinate and Vectors in Space
   • terminology: octants, the first being where x, y, and z are all positive.
   • right-handed systems
   • points are `(x,y,z)`
   • Microsoft Mathematics at http://www.microsoft.com/en-us/download/details.aspx?id=15702
   • distance between points `p=(x_1,y_1,z_1) and q=(x_2,y_2,z_2)` is given as `sqrt((x_2-x_1)^2 + (y_2-y_1)^2 + (z_2-z_1)^2)`.
   • midpoint between points `p=(x_1,y_1,z_1) and q=(x_2,y_2,z_2)` is given as the point `((x_1+x_2)/2,(y_1+y_2)/2,(z_1+z_2)/2)`.
   • Equation of sphere given two points on the diameter of the sphere (see the SPHERE3 TI program).
   • Equation of sphere given 4 points on the sphere: solving systems of linear equations; rref. (see the SPHERE TI program) Actually, start by looking at the special page for the general case.
   • standard unit vectors i, j, k or `vec i, vec j, vec k`
   • unit vector in same direction as a given vecor. say we have `bbv = \ltx,y,z\gt` then the unit vector in the same direction as v is `\lt x/(||bbv||),y/(||bbv||),z/(||bbv||)\gt`.
   • component form to compare vectors in non-standard position.
   • Remember that vectors have magnitude and direction but not location. We say that two vectors are parallel if they differ only by magnitude, that is, they have the same direction. But that means, for non-zero vectors, that v is parallel to u if and only if we can find some scalar c such that v=cu.
   • We can use the requirement for being parallel to find colinear points or to determine if three, or more, points are colinear.
   • Note that this will come back in section 11.5 when we get parametric forms of a line in space.
3. Section 11.3: The Dot Product of two Vectors
   • Define the dot product: for `bbu=\ltu_1,u_2\gt` and `bbv=\ltv_1,v_2\gt` we have `bbu * bbv = u_1**v_1 + u_2**v_2`;
     for `bbu=\ltu_1,u_2,u_3\gt and bbv=\ltv_1,v_2,v_3\gt` we have `bbu * bbv = u_1**v_1 + u_2**v_2 + u_3**v_3`
     and so on for even higher dimensions. Note that the dot product is a scalar.
   • properties of dot product
     1. u • v = v • u
     2. u • (v + w ) = u • v + u • w
     3. c(u • v) = cu • v = u • cv
     4. 0 • v = 0
     5. v • v = ||v||²
   • Angle between non-zero vectors `cos\quad theta = (bbu*bbv)/(||bbu||\quad||bbv||)`
     * (note that the angle θ must be 0 ≤ θ ≤ π). The derivation of this depends on the law of cosines and the properties of the dot product. (See the derivation page for the details.)
   • We could rewrite that as `bbu*bbv = ||bbu||**||bbv||\quadcos\quadtheta`.
   • orthogonal `bbu*bbv=bb0`
   • Direction cosines:
     If we "place" a vector `bbv=\ltv_1,v_2,v_3\gt` starting at the origin, we can look at the angles between `bbv` and the vectors `bbi, \quad bbj, and bbk`. We call these angles `alpha, \quad beta, and gamma` respectively. Then, for example,
     `bbv*bbi=||bbv||\quad||bbi||\quad cos(alpha) = ||bbv||\quad cos(alpha)` but
     `bbv*bbi=\ltv_1,v_2,v_3\gt*\lt1,0,0\gt = v_1` so
     `||bbv||\quad cos(alpha) = v_1`
     We could do this for all three directions and solve these for the cosine vaue to get:
     For `bbv=\ltv_1,v_2,v_3>` we have `cos(alpha)=v_1 / (||bbv||)`; `cos(beta)=v_2 / (||bbv||)`; `cos(gamma)=v_3 /(||bbv||)`
     This gives us `alpha=arccos(v_1 / (||bbv||))`; `beta=arccos( v_2 / (||bbv||))`; `gamma=arccos( v_3 / (||bbv||))`;
   • Projections: projection of u onto v denoted as proj_vu
     The idea is to "cast the 90º shadow" of u onto a vector w₁, that is a scalar multple of vector v. Consider the following diagram:
     
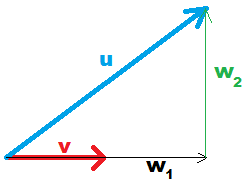
     Here w₁=proj _v u.
     We have `bbw_1 = cbbv`, for some scalar c, and
     `bbu=bbw_1+bbw_2`, so
     `bbu=cbbv+bbw_2`. Therefore, we can form the dot product
     `bbu*bbv=(cbbv+bbw_2)*bbv`. But that is the same as
     `bbu*bbv=(cbbv*bbv)+(bbw_2*bbv)`. Given that `bbw_2` is orthogonal to `bbv` we know that `bbw_2*bbv=0`, thus, `bbu*bbv=c||bbv||^2`, or
     `c=(bbu*bbv)/(||bbv||^2)`. Remember that `bbw_1=cbbv` and we get `proj_(bbv)bbu =bbw_1=( (bbu*bbv)/(||bbv||^2))bbv`.
   • w₂ as "vector component of u orthogonal to v", `bbw_2 = bbu - bbw_1`.
   • See TI program Threesp (ignoring menu 1 item 4)
   • Work
     • defined as W=(amount of force)(distance moved)
     • `W=||bbF||\quad ||vec(PQ)||`
     • `W=||proj_(vec(PQ))bbF||\quad ||vec(PQ)||`
     • `W=cos(theta)||bbF||\quad ||vec(PQ)||`
     • `W=bbF*vec(PQ)`
4. Section 11.4: The Cross Product of Two Vectors in Space
   • define cross product (note: only in 3-space)
   • The determinant "form" as a way to remember the definition
     `bbu xx bbv = |[bbi,bbj,bbk],[u_1,u_2,u_3],[v_1,v_2,v_3]| = (u_2**v_3 - u_3**v_2) bbi - (u_1**v_3 -u_3**v_1) bbj + (u_1**v_2 - u_2**v_1)bbk`
   • When dealing with determinants we have both numeric instances and symbolic instances
   • properties of the cross product
     1. u v = ^–(v u)
        and the consequence with respect to right-handed vs. left-handed
        (see * in definition of angle between vectors) Note that `bbu, bbv, and bbu\timesbbv` form a right-handed system while `bbu, bbv, and bbv\timesbbu` form a left-handed system.
     2. u (v + w) = (u v ) + ( u w)
     3. c(u v) = (cu) v = u (cv)
     4. u 0 = 0 u = 0
     5. u u = 0
     6. u • (v w) = (u v) • w
   • Geometric Properties of the cross product for non-zero vectors u and v
     1. u v is orthogonal to both u and v
     2. ||u v|| = ||u||*||v||*sin( θ ), where θ is the angle from u to v.
     3. u v = 0 if and only if u and v are scalar multiples of each other
     4. ||u v|| = area of the parallelogram having u and v as adjacent sides.
   • The triple scalar product u • ( v w )
   • The triple scalar product is a scalar.
   • It turns out that the triple scalar product is equal to the determinant of the components, that is
     if `bbu=\ltu_1,u_2,u_3\gt,\quadbbv=\ltv_1,v_2,v_3\gt, and \quadbbw=\ltw_1,w_2,w_3\gt` then
     `bbu*(bbvxxbbw)= |[u_1,u_2,u_3],[v_1,v_2,v_3],[w_1,w_2,w_3]|`
   • volume of parallelpiped defined by the three vectors that represent its edges is the absolute value of the triple scalar product of the three vectors, that is,
     Volume of parallelpiped is `|bbu * (bbv xx bbw)|`.
   • Getting equivalent forms: u • ( v w ) = v • ( w u ) = w • ( u v )
   • Vectors3 (anything missing?)
5. Section 11.5: Lines and Planes in Space
   If we have a vector `bbv=\lt a,b,c \gt` and we want to specify a line `bbL` that is "parallel" to `bbv` and it contains the point `bbP=(x_1,y_1,z_1)` then for any other point on the line, `bbQ=(x,y,z)` it must be the case that `vec(PQ)` is parallel to `bbv`, but that means that `vec(PQ)=tbbv`, for some scalar `t`.
   We know that `vec(PQ) = \lt(x-x_1),(y-y_1),(z-z_1)\gt ` and, at the same time, `vec(PQ)=tbbv = t\lta,b,c\gt = \ltta,tb,tc\gt`. But this gives us
   `x-x_1=ta and y-y_1=tb and z-z_1=tc` or
   `x-x_1=at and y-y_1=bt and z-z_1=ct` or
   `x=x_1+ta and y=y_1+tb and z=z_1+tc`
   See: http://cs.jsu.edu/~leathrum/Mathlets/parapath.html
   • Symmetric equations of line (if ALL direction numbers are non-zero)
     `(x-x_1)/a=t and (y-y_1)/b=t and (z-z_1)/c=t`, so
     `(x-x_1)/a=(y-y_1)/b= (z-z_1)/c`
   • Equation of plane. Note that once we have a plane we define any vector that is perpendicular to the plane to be a normal vector. So, from any point `bbP=(x_1,y_1,z_1)` on the plane, the set of all points `bbQ=(x,y,z)` on the plane must satisfy the requirement that the vector from `bbP` to `bbQ` must be perpendicular to a normal vector, call it `bbn=\lta,b,c\gt`. That means that the dot product of the two vectors must be 0. This gives rise to the standard form of the equation of a plane in 3-space.
     Standard form `bbn*vec(PQ)=a(x-x_1)+b(y-y_1)+c(z-z_1)=0`
     General form ax +by +cz + d = 0 (also as ax +by +cz = d, but a different d)
   • angle θ between two planes (0≤θ≤π/2) is defined to be the angle between the normal vectors to the plane. So, if we have two planes and the corresponding normal vectors, `bbn_1 and bbn_2` then we have
     `cos\quadtheta = (|bbn_1*bbn_2|)/(||bbn_1||**||bbn__2||)`, note the absolute value in the numerator because the angle between two planes is always less than π/2.
   • Parametric line of intersection of two planes: can "solve" the pair of equations to get one variable in terms of another (i.e., eliminate one of the three and solve for the one of the remaining in terms of the other remaining, then substitute that relation back into one of the originals and you get the eliminated variable as a function of the "other remaining" so now we can set the originally eliminated to be "t" and express the others in terms of "t". Or, just look at the cross product of the two normal vectors to get the directional numbers for the line of intersection, but then we still need to find a point on the intersection line so that we can adjust the parametric equations. However, there is an easy way to find two points on the intersection line by introducing two new planes and using rref(). In any case, the example in the book is hopelessly misleading because in that example the intersection contains the origin. See the pencast for finding the line of intersection for more information.
   • Distance from point to plane (given by ax + by + cz +d =0, note the position of d): Q=(x₀, y₀,z₀) a point not in plane, P a point in plane, n a vector normal to plane
     `dist=||proj_(bbn)vec(PQ)||`
     `dist=(|vec(PQ)*bbn|)/(||bbn||) `
     `dist=(|a(x_0-x)+b(y_0-y)+c(z_0-z)|)/sqrt(a^2+b^2+c^2)`
     `dist=(|ax_0 +by_0 +cz_0 -(ax+by+cz)|)/sqrt(a^2+b^2+c^2)`
     `dist=(|ax_0 +by_0 +cz_0 +d|)/sqrt(a^2+b^2+c^2)`
     
   • Distance from point to line: Q a point not on line, P a point on line, `bbu` a direction vector for the line
     `dist=||vec(PQ)||sin(theta)` ; `theta` is the angle between `vec(PQ) and bbu`. But we know that `||bbuxxvec(PQ)|| = ||u||\quad||vec(PQ)||\quadsin(theta)`, so
     `dist = ||vec(PQ)|| \quad sin(theta)=(||vec(PQ)xxbbu||)/(||bbu||)`
6. Section 11.6: Surfaces in Space
   • Cylindical Surfaces
     Definition of cylindrical surface (need not look at all like a cylinder)
     directrix or generating curve
     rulings
     perpendicular to basic plane or angled?
     If perpendicular then it will only use the variables of that basic plane.
   • Quadric Surfaces
     general form: `Ax^2 +By^2 + Cz^2 + Dxy + Exz +Fyz + Gx + Hy + Iz +J = 0`
     standard form, when we have no cross product terms, `((x-a)^2/e) +- ((y-b)^2/f) +- ((z-c)^2/g) = h`
     traces
     where did the xy, yz, and xz terms go?
     

     Ellipsoid `x^2/9 + y^2/16 +z^2/4 = 1`	Elliptic Cone `x^2/9 + y^2/16 +z^2/4 = 0`
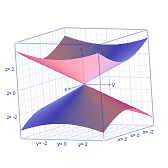
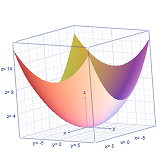
     Hyperboloid One Sheet `x^2/9 + y^2/16 - z^2/4 = 1`	Elliptic Paraboloid `x^2/9 + y^2/16 = z`
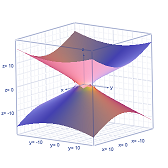
     Hyperboloid Two Sheets `x^2/9 - y^2/16 - z^2/4 = 1`	Hyperbolic Paraboloid `x^2/9 - y^2/16 = z`

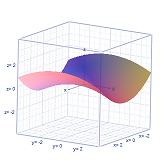
   • Surfaces of Revolution
     If what we want is a surface that is a function along one axis, then we will need a generating curve in some basic plane, that is a function.
     Discuss: y=3x+4 vs f(x)=3x+4 vs y=f(x) vs f={(x,y)|y=3x+4}
     1. First, if we are going to revolve a generating curve that is in the xy-plane (and has y as a function of x), then for any specific x value, we will know the y value by evaluating that function. Furthermore, for that given x value, the curve will be a circle of radius f(x). But that means that y² + z² = radius² or y² + z²=(f(x))²
     2. Then, in general, instead of using f(x) we could call the function r(x) to show that it determines the radius based on the value of x.
     3. y² + z² = [ r(x) ]² ; revolve around x-axis
        --to have the generating curve in x-y plane we would have some y=r(x), but we still need to put the r(x) into [ r(x) ]² in the general form.
        --to have the generating curve in x-z plane we would have some z=r(x), but we still need to put the r(x) into [ r(x) ]² in the general form.
     4. x² + z² = [ r(y) ]² ; revolve around y-axis
     5. x² + y² = [ r(z) ]² ; revolve around z-axis
7. Section 11.7: Cylindrical and Spherical Coordinates
   • Cylindrical Coordinates (r, θ, z)
     Cylindrical to rectangular:
         x=r cos(θ),   y=r sin(θ),   z=z
     Rectangular to Cylindrical
         r² = x² + y²,   tan(θ) = (y/x),   z=z
   • Spherical Coordinates (Not a universal standard) (ρ, θ, φ)
     See http://random-science-tools.com/maths/coordinate-converter.htm
     See http://en.wikipedia.org/wiki/Spherical_coordinate_system
     Spherical to Rectangular:
         x = ρ sin(φ) cos(θ),   y= ρ sin(φ) sin(θ),   z= ρ cos(φ)
     Rectangualr to Spherical:
         ρ² = x² + y² + z²,   tan(θ) = (y/x),   φ = cos^–1( z / sqrt(x²+y²+z²) )
     
     
     Spherical to Cylindrical (r≥0)
         r² = ρ² sin²(φ),   θ = θ,   z = ρ cos(φ)
     Cylindrical to Spherical (r≥0)
         ρ = sqrt(r² + z²),   θ = θ,   φ = cos^–1( z / sqrt(r²+z²) )