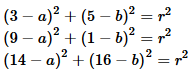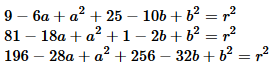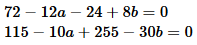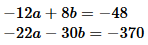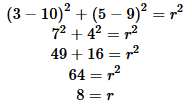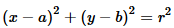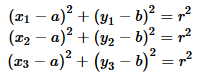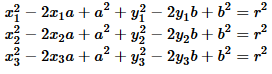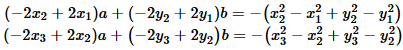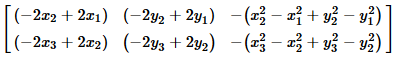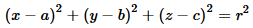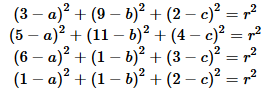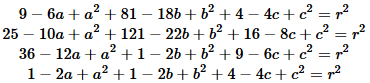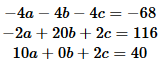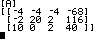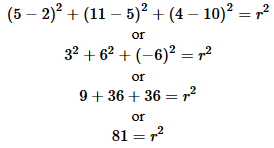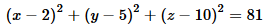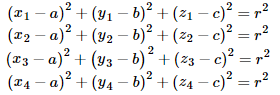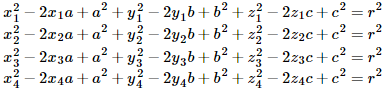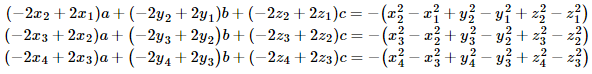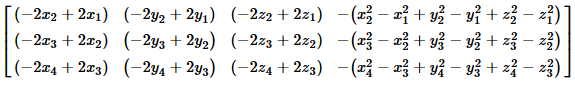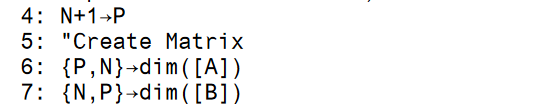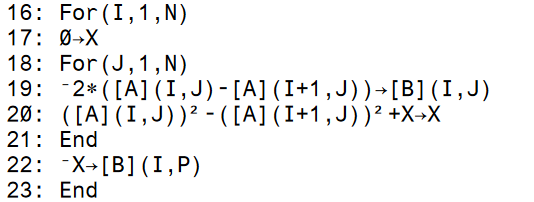Circles, Spheres, and Hyper-Spheres
This page presents the problem of finding the equation of a
- circle in two space, given three non-colinear points;
- sphere in three space, given four non-coplanar points;
- hyper-sphere in n-space given (n+1) non-cohyperplanar points.
Circle
The general equation of a circle in two-space is
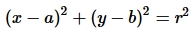 where the center of the circle is at the point (a,b) and
the radius of the circle is r. Our task is to find the
values of a, b, and r
if we are given three non-colinear
points on the circle.
[Note that if they are on the circle then they cannot
be colinear.]
where the center of the circle is at the point (a,b) and
the radius of the circle is r. Our task is to find the
values of a, b, and r
if we are given three non-colinear
points on the circle.
[Note that if they are on the circle then they cannot
be colinear.]
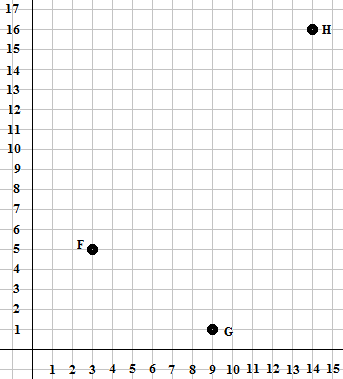
As an explicit example,
consider the points F=(3,5), G=(9,1), and H=(14,16).
We would graph the points as in Figure 1.
Figure 1
Then we would find the midpoint of the segment FG,
this turns out to be
the point (6,3) and we would construct the
perpendicular bisector of the segment FG.
We woud do the same for the segment FH, finding the midpoint at
(8.5,10.5), and construct the perpendicular bisector to FH.
These are all shown in Figure 2.
Figure 2
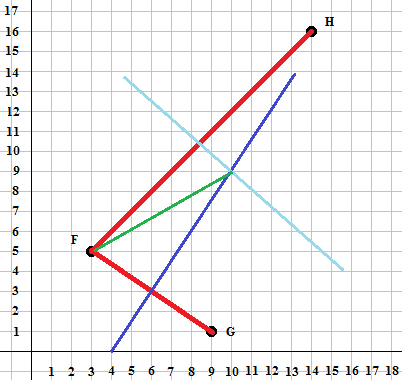
The point where the two perpendicular bisectors
of chords of the circle
intersect is the center of the circle, clearly
at (10,9) in Figure 2.
And a radius of the circle would be the
line segment from the center to the point F,
also shown in Figure 2.
Using the Pythagorean Theorem, we would find that
the length of the radius is 8.
From this we find that the equation of the circle is
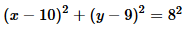 .
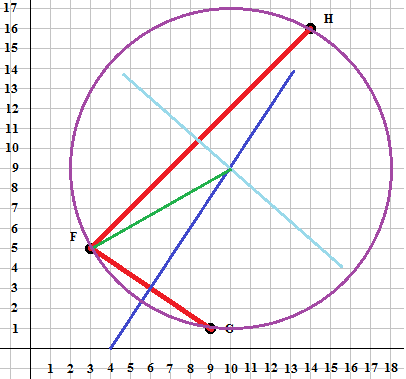
If we construct such a circle we get the image shown in Figure 3.
Figure 3
.
If we construct such a circle we get the image shown in Figure 3.
Figure 3
Let us return to the original problem statement
and solve this via algebra.
First, we know that the points F, G, and H are all
points on the circle.
Thus, we can substitute the coordinates of any of
those points into the equation
for the circle. Therefore, we have the following three equations,
all of which are true:
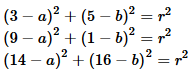 Notice that these are three equations in 3 unknowns,
a, b, and r.
Expanding the three equations gives us
Notice that these are three equations in 3 unknowns,
a, b, and r.
Expanding the three equations gives us
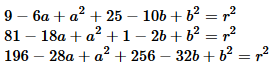 Again, three equations in three unknowns.
Unfortunately, these are quadratic equations.
We would really prefer to be dealing with linear equations.
We form new equations
by finding the difference between the second and first and
then the difference between the third and the second
equations. This gives us
Again, three equations in three unknowns.
Unfortunately, these are quadratic equations.
We would really prefer to be dealing with linear equations.
We form new equations
by finding the difference between the second and first and
then the difference between the third and the second
equations. This gives us
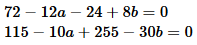 These simplify to
These simplify to
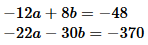 These are two linear equations in two unknowns.
We can solve this on the calculator using a matrix and
the rref function as shown in Figure 4.
Figure 4
These are two linear equations in two unknowns.
We can solve this on the calculator using a matrix and
the rref function as shown in Figure 4.
Figure 4

This means that the value of a is 10
and the value of b is 9,
meaning that the center of the circle is at (10,9).
All that remains is to find the value of r.
We can do that from any of the three original equations now that we know
the value of a and b.
Using the first equation we now have
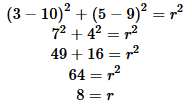
The process that we just used,
- state the general equation of a circle
with center at (a,b) and radius r;
- form the three quadratic equations,
having unkowns a, b,
and r, by using the general equation
for the circle but substituting the
coordinates of the three given points for
the values of x and y;
- expand those three equations,
- form two linear equations,
with unknowns a and b,
by taking the difference between the second and first
quadratic and then the difference between the
third and the second quadratic;
- put those two linear equations into standard form;
- represent those two linear equations via a 2x3 matrix;
- solve that matrix using rref() to obtain the values of
a and b;
- use any one of the original
quadratic equations to solve for r.
is a general solution.
That is, there was nothing special
about the values of the three original
points that allowed us to change the
three quadratic equations into two linear
equations in two unknowns.
We can restate the solution for finding the equation of a circle
given three points on the circle as
(x1,y1,
(x2,y2, and
(x3,y3 by
stating the general form of the circle
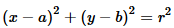
forming the three quadratic equations
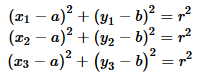
expanding the quadratic equations
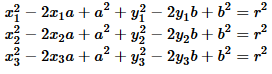
forming and simplifying the two linear equations
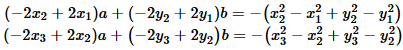
and forming the reprentaive matrix
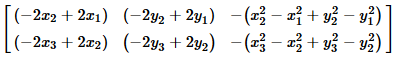
and then solving this via the rref() function.
Sphere
The general equation of a sphere in 3-space with center at
(a,b,c), is
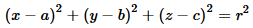
If we have 4 non-coplaner points in 3-space then there is
a unique sphere that has those points on its surface.
Or, if we know the coordinates of four points on a sphere then
we should be able to find the equation of the sphere.
Although there is a geometric solution to this problem, one that
follows the pattern of the geometric solution
to finding the equation of a circle
from the three points on the circle,
it is difficult to draw such a solution.
Rather, we will just expand on the
algebraic solution pattern
that we just saw. We can start with a specific problem.
Consider the four points (3,9,2), (5,11,4), (6,1,3) and (1,1,2).
To find the equation of the sphere with those points on its surface
we form the four quadratic equations
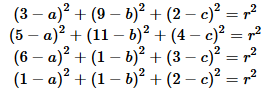 We expand those equations to get
We expand those equations to get
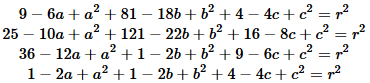 From there we form three linear equations by finding the difference of the second and first quadratic equation,
the difference of the third and second quadratic equation, and the difference of the
fourth and the third quadratic equation.
Once simplified this becomes
From there we form three linear equations by finding the difference of the second and first quadratic equation,
the difference of the third and second quadratic equation, and the difference of the
fourth and the third quadratic equation.
Once simplified this becomes
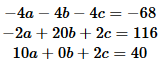 We can rewrite this as a 3x4 matrix
We can rewrite this as a 3x4 matrix
 which we can put into the calculator as
which we can put into the calculator as
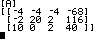 and then we can use rref() to solve that system, getting
and then we can use rref() to solve that system, getting
 Thus the center of the circle is at the point (2,5,10).
We can get the radius by rewriting one of the original quadratic equations using the
actual center values. Here we will use the second equation which becomes
Thus the center of the circle is at the point (2,5,10).
We can get the radius by rewriting one of the original quadratic equations using the
actual center values. Here we will use the second equation which becomes
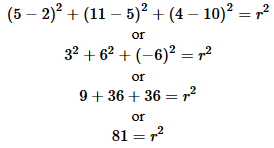 Thus the radius of the circle is 9 and the final equation of the circle
is
Thus the radius of the circle is 9 and the final equation of the circle
is
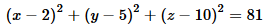
We can actually do this same problem, at least to the point of setting
up the matrix of values, for the general case of having four points
(x1,y1,z1),
(x2,y2,z2),
(x3,y3,z3), and
(x4,y4,z4).
Using those points we get four quadratic equations
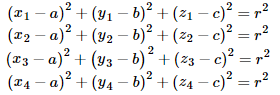 and these expand to
and these expand to
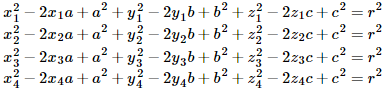 From those equations, by finding the difference between the second and the first,
the third and the second, and the fourth and third,
we get three linear equations
From those equations, by finding the difference between the second and the first,
the third and the second, and the fourth and third,
we get three linear equations
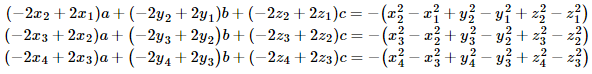 We can rewrite them as the matrix
We can rewrite them as the matrix
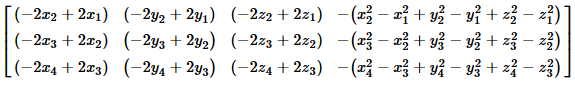 For any four points with numeric cootdinates this resolves to
a 3 by 4 numeric matrix that we can enter into the calculator and
then solve via rref().
For any four points with numeric cootdinates this resolves to
a 3 by 4 numeric matrix that we can enter into the calculator and
then solve via rref().
Hypersphere and the program SPHERE
Notice the pattern in both the development of
our generalized matrix solution and of the variables shown
in the resulting matrix.
Although we may not be able to visualize moving into 4 dimensions,
the pattern of our discussions, first for the circle
and then for the sphere, will certainly repeat, but it will
be expanded to have 5 points in 4-space producing 5 quadratic equations.
Then by finding the differences between successive pairs of those 5
quadratic equations we will get 4 linear equations in 4 unknowns,
which we can then represent in a 4x5 matrix that we can again solve
via rref() to find the coordinates of the center
of a hypersphere, the set of all points at some given
distance from that center.
This is the sort of pattern that we can capture in a program.
The SPHERE program for our TI-83/84 calculators does this.
The program opens by displaying a title and asking for the number
of dimensions in our problem:
 The program keeps that value in the variable N.
But if we have N then we need N+1
points, each of which has N dimensions. The program goes on to
store the value N+1 in the variable P.
We can use N and P to create two matrices,
one to hold the coordinates of the points and one to hold the
values representing the N linear equations that
we would get via our process:
The program keeps that value in the variable N.
But if we have N then we need N+1
points, each of which has N dimensions. The program goes on to
store the value N+1 in the variable P.
We can use N and P to create two matrices,
one to hold the coordinates of the points and one to hold the
values representing the N linear equations that
we would get via our process:
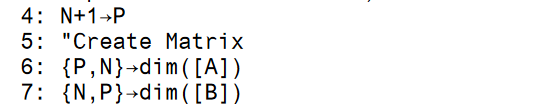 The matrix [A] is now a PxN matrix.
As such it can hold N coordinates for each of the
P points. The net part of the program
cycles through each of those P points asking the user
for each of the N coordinates.
The matrix [A] is now a PxN matrix.
As such it can hold N coordinates for each of the
P points. The net part of the program
cycles through each of those P points asking the user
for each of the N coordinates.
 At the end of that process [A] holds
all
of the cooordinates for all of the points.
At the end of that process [A] holds
all
of the cooordinates for all of the points.
The next task is to compute the coefficients and the
constant value for each of the N linear
equations.
We use the pattern that we have seen in the case of the
circle and the sphere to compute these.
To find the coefficinet we remember that when we square the
terms in the quadratic equation we get a middle term
with the coefficient that looks like -2*wi
where wi is the ith coordinate
of the known point.
Therefore, we code subtracting the (i+1)st
equation from the ith by using
line 19 of the program to pick out the appropriate
values from [A} and assign -2
times that difference to the appropriate
location in [B].
(A small note: in the exmples from the
start of the page we have
subtracted the ith>
equation from the (i+1)st,
but the program does it reversed.
As long as we are consistent, the change is immaterial to the
final result.)
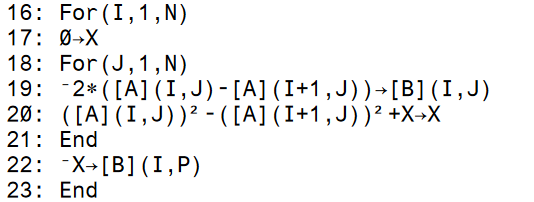 Finding the constant values for each of the linear equations,
the P value in each row of [B],
is just finding the sum of the
differences of each of the squares of the known point
coordiantes.
The program does this by initializing X to 0
at line 17 and then accumulating the sum in line 20.
Finally, the sum is assigned to the correct
location in [B] at line 22.
Finding the constant values for each of the linear equations,
the P value in each row of [B],
is just finding the sum of the
differences of each of the squares of the known point
coordiantes.
The program does this by initializing X to 0
at line 17 and then accumulating the sum in line 20.
Finally, the sum is assigned to the correct
location in [B] at line 22.
Line 20 of the program performs the rref()
function on the matrix [B] and stores that in
matrix [C].
The final column of [C] now holds the
coordinates of the center of the hypersphere.
All that remains is to display the coordinates
of the center and to find the radius and to do that we
compute the distance from the center to
one of the points.
The For End construction from line 27
through line 30
not only displays the coordinates of the center,
it also builds up the
squares of the differences between coordinates of
the first point and coordinates of the center.
That accumulated sum is the square of the radius
and is displayed via line 31.
 Thus the program happily wrks for 2, 3, or more dimension problems.
Thus the program happily wrks for 2, 3, or more dimension problems.
©Roger M. Palay
Saline, MI 48176
May, 2016

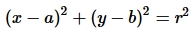 where the center of the circle is at the point (a,b) and
the radius of the circle is r. Our task is to find the
values of a, b, and r
if we are given three non-colinear
points on the circle.
[Note that if they are on the circle then they cannot
be colinear.]
where the center of the circle is at the point (a,b) and
the radius of the circle is r. Our task is to find the
values of a, b, and r
if we are given three non-colinear
points on the circle.
[Note that if they are on the circle then they cannot
be colinear.]


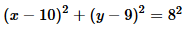 .
If we construct such a circle we get the image shown in Figure 3.
.
If we construct such a circle we get the image shown in Figure 3.