Angle Between Two Vectors

Return to the Chapter 11 Topics page
Revised May 27, 2014

Some images on this page have been generated via AsciiMathML.js.
For more information see: www.chapman.edu/~jipsen/asciimath.html.

We are given two vectors `bbu` and `bbv` in two space and we are asked to find the angle, `theta` between them. What we come up with is the following:

`cos \quad theta = (bbu * bbv )/(||bbu|| \quad ||bbv||)` What we know about the dot product includes the dot product definition:
For u=<u₁,u₂> and v=<v₁,v₂>
we have u • v=u₁*v₁ + u₂*v₂
the dot product properties:

u • v = v • u
u • (v + w ) = u • v + u • w, and its corrolary
u • (v – w ) = u • v – u • w
c(u • v) = cu • v = u • cv
0 • v = 0
v • v = ||v||²

For two vectors u and v we could locaate representatives of these vectors having a common initial point, as in the image

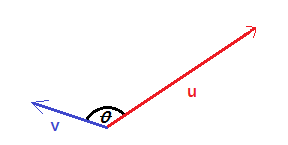Of course, with those two vectors we could create the vector u – v and place it as in the following image:

It is clear that we now have a triangle. In fact, we have a triangle with sides a, b, and c. One of the many relationships that we have for triangles is the law of cosines. For our triangle that would be
c²=a² + b² - 2(a)(b)cos(θ)
but
c=||u – v||,
a=||u|| and
b=||v||.
Substituting those values we can restate the law of cosines as
`||bbu - bbv||^2 = ||bbu||^2 + ||bbv||^2 - 2\quad ||u|| \quad ||bbv|| cos( theta )`
The left side of that equality is just the square of the magnitude of a vector, in this case `bbu-bbv`. However, from the fifth dot product property we know that the square of the magnitude of a vector is equal to the dot product of the vector with itself. Thus,
`||bbu - bbv||^2 = (bbu-bbv)*(bbu-bbv)`. The dot product on the right could be written, just for the moment, as
`bbw * (bbu-bbv)`, where we have replaced the first factor, `(bbu-bbv)`, by `bbw` but we have left the right factor as is. This, then, conforms to the second dot product property which lets us distribute the dot product over the subtraction. Our equality then becomes
`||bbu - bbv||^2 = bbw*(bbu-bbv) = bbw*bbu - bbw*bbv`.
Reverting to the meaning of `bbw` as `(bbu-bbv)`, this becomes `||bbu - bbv||^2 = (bbu-bbv)*bbu - (bbu-bbv)*bbv`.
Then, just to be formal we can use the commutative property(#1) to rewrite this as `||bbu - bbv||^2 = bbu*(bbu-bbv) - bbv*(bbu-bbv)`.
Again, employing the distributive property for each term, we can expand this to `||bbu - bbv||^2 = (bbu*bbu-bbu*bbv) - (bbv*bbu-bbv*bbv)`.
However, using property #5 we can change this to `||bbu - bbv||^2 = ||bbu||^2 - bbu*bbv -bbv*bbu +||bbv||^2`.
Using the commutative property on the third term we change this to `||bbu - bbv||^2 = ||bbu||^2 - bbu*bbv -bbu*bbv +||bbv||^2`.
Then, we rearrange and combine values to get `||bbu - bbv||^2 = ||bbu||^2 + ||bbv||^2-2bbu*bbv`.

Now recall that we started with the law of cosines applied to our triangle as
`||bbu - bbv||^2 = ||bbu||^2 + ||bbv||^2 - 2\quad ||u|| \quad ||bbv|| cos( theta )`
and we just expaned the left side to get
`||bbu - bbv||^2 = ||bbu||^2 + ||bbv||^2-2bbu*bbv`.
Therefore,
`||bbu||^2 + ||bbv||^2-2bbu*bbv = ||bbu||^2 + ||bbv||^2 - 2\quad ||u|| \quad ||bbv|| cos( theta )`
This simplifies to
`-2bbu*bbv = -2\quad ||u|| \quad ||bbv|| cos( theta )`
which, in turn, becomes
`cos(theta)= (bbu*bbv)/(||bbu|| \quad ||bbv||)`.
Of course, if we are actually looking for `theta` then we want to rewrite this as
`theta = arccos((bbu*bbv)/(||bbu|| \quad ||bbv||))`.

Return to the Chapter 11 Topics page