Chapter 3 Notes for Math 181
Finite Mathematics, Fifth Edition

In order to tie comments to specific locations in the book, I have used the available page ruler sheet to identify lines in the text. A copy of that page ruler sheet can be printed from The Index Sheet.

Chapter 3: Matrices
3.1 Matrix Adition and Scalar Multiplication and Transpose
Page	Line #	Notes
182	22	The book is actually quite good at emphasizing the Row-Column order convention for refering not only to the matrix but also to the entries in the matrix. Thus, an m x n matrix always has m rows and n columns. The entry in matrix A in its ith row and jth column is referred to as entry Aij. This will carry over to the calculator, but there we do not have the luxury of bold, italics, or subscripts. On the TI-83 family calculators, the matricies appear as [A], a single symbol found in the MATRIX window. The entry in row I and column J of matrix [A] is refered to as [A](I,J).
182	26	The book mentions the equality of matrices here. It should be emphasized a bit. Two matrices are equal if and ony if they have the same dimensions (the same number of rows and the same number of columns) and the corresponding entries are the same value in every case. The book points out that a 3 x 5 matrix can never equal a 3 x 4 matrix. This is clear since there are 15 entries in the first and only 12 in the second. It is also the case that a 3 x 4 matrix can never equal a 4 x 3 matrix, even though they have the same number of entries. Even in a special case where all entries in both matrices have the same value, such as 1, item (3,4) of the first matrix [the item in row 3 column 4], just has no corresponding entry in the second matrix, which after all only has 3 columns.
184	19	We do have a web page that illustrates the addition, subtraction, and scalar multiplication of matrices on the TI-83 family of calculators. This also talks about doing a transpose of a matrix.
3.2 Matrix Multiplication
Page	Line #	Notes
192	12	The question posed (Why a row and a column?) is most. appropriate. They book is using this simple example of having a single row and a single column, viewed as matrices, as a way to introduce the complely non-intuitive algorithm for matrix multiplication. In fact, given the example used in the book, there are more appropriate ways to represent the problem. The reader of the book needs to just go along with what seems to be an overly complex way to set up the problem.
196	8	In reading the part of the text that follows "Look at the dimensions in the two Quick Examples on the previous page" one might miss reading the important word "dimensions" in the sentence. What follows that text refers to the dimensions of the four matrices on the previous page. It might have been better had the book given a second hint, as in:
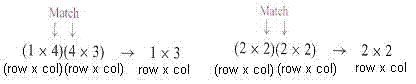		The page on matrix multiplication and other topics might be of some help here. It also covers a bit of the Matrix Inversion from the next section.
3.3. Matrix Inversion
Page	Line #	Notes
206	all	The page on matix inversion might be of some help here. That page goes over the steps to find the inverse of a matrix, along with a few more issues about solving for an inverse.
3.4 Game Theory
Page	Line #	Notes
217	all	There has been a request for a web page giving an example of a game theory problem that might be on the test. Such a page has been created. Please look at the game theory page, but realize that this is a new page and that it might need some revision. Please provide feedback giving me your thoughts on the material on the page.
3.5 Input-Output Models
Page	Line #	Notes
2	36
2	36