Chapter 1 Introduction to Detailed Notes

These are notes that I made on my reading of the textbook. There is no real attempt to have comments on absolutely everything in the book noted here. At the same time, there is supplementary material here that is not in the book.

After writing out the notes for the first few sections, it has become clear that there is a tendency to make this a "teaching" document. As much as possible, efforts will be made to not do this. Rather, if there is teaching material to be presented then that will be done in separate pages, with pointers inserted here.

As of January, 2000, there are two versions of the 9th edition. Version 1 has the heading "BASIC FUNCTIONS" on the inside of the front cover. Version 2 replaces that heading with "BASIC RELATIONS and FUNCTIONS". Many of the errors of version 1 have been fixed in version 2. In those cases where these notes point out errors in version 1 that have been fixed in version 2, I am attempting to include reference to that change in these notes.

Chapter 1: Algebra of Numbers and Functions

Chapter 1, Section 0: Review of Algebraic Expressions

Note that the material in this section is entirely new to this text. Therefore, it is likely to have a number of errors in it.

In version 1 only

In fact, on page 1, Example 1 has two typographic errors; namely, the problem statement should conclude with, when x=2, y=-1/2, and z=-3 without reference to values for b and c.

It would be worth doing this example on the calculator. See page 1p0e1 for the key strokes and display for this on the TI-85 or TI-86.

See page 1p0e2 for the steps needed to do Example 2 on the calculator. That page not only introduces the

command but also demonstrates the steps needed to put a shortcut to the

command into the CUSTOM menu on the TI-85 and TI-86 calcualtors. On the calculator used to make the images in the textbook, that step was done prior to the calculator image given for in Example 4 of the textbook.

Example 3 can not be done directly on the TI-86, however, we can use the calculator to check our work in doing such problems. See 1p0e3 for the key strokes and display that can be used to check the work in Example 3.

In version 1 only

Note: The work in the text is incorrect. By checking the problem on the calculator we are able to not only determine that there is an error, but we can find out where the error takes place. The correct answer is a(c-b²)/(a-b).

Example 4 on page 2 includes a screen dump from a TI-86 as an answer. Note that the first two lines on the calculator screen are left over from some earlier work. Also, note that the example uses the evalF function on the TI-86. The page 1p0e4 first goes through the steps needed to produce that result, and then that page demonstrates doing the problem without using the evalF function, much as we had done with Example 1. It is important to know that there are different ways to do these problems and to see the advantages of each method.

In version 1 only

In Example 5 we see one of the many times that we in mathematics use some seemingly confusing notations. The example starts with Let x=x-h when, in fact we do not mean that at all. Rather, we are really saying Let x be replaced by x-h in the expression x²-7x+3 That gives rise to the new expression (x-h)²-7(x-h)+3 which then simplifies to x²-2hx +h²-7x+7h+3

In the middle of page 3, after the word "Furthermore," insert the statement (if the index is missing it is assumed to be 2)

Some note should be made of the fact that we can use these properties in either direction. That is given

we can say it is equal to

which is equal to

. However, given

we can say that it is equal to

Note that in the last two lines of the page, I prefer adding the word "providing" before the condition regarding the value of b. Thus, I would like to see the statement as: with the same restrictions by index for n being either odd or even, and providing that we have b0.

Examples 6 and 7 on page 4 use the properties introduced on the previous page. We can, and should, use the calculator to check our work. The following two screen imges demonstrate checking Examples 6 and 7 on the calculator.

The TI-85 and TI-86 do allow us to check our simplification of roots by comparing the numerical values of the expressions before and after simplification. These calculators do not directly simplify radicals. However, we can write programs for these calculators, and we can design those programs to do many of the tasks that are not built into the TI-85 and TI-86. As an example, you might want to look at the page reducerad for a program listing and description (as well as a link for downloading the program if you have a TI-GraphLink Cable). A companion program to find the prime factorization of an integer is given on the page primefact.

Examples 8, 9, and 10 are extremely important. There are many times in this course and in the Calculus courses when we will want to rationalize numerators or denominators. Example 8 demonstrates a case where we are dealing with a square root. It is sufficient to multiply the expression by the value of 1 in the form of the square root of 2 divided by iteslf. As a result, the denominator becomes the square root of 2 squared, or just 2.

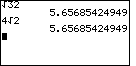Example 9 demonstrates the third root of a value. Again, we want to multiply the expression by 1 in the form of a number divided by itself. The tendency for many students is to multiply the given expression by the third root of seven divided by itself. This tendency follows the pattern set in Example 8. However, in Example 9 we are working with the third root, not the square root. Therefore, to rationalize a value, we need to produce the third root of the value cubed. In Example 9 this means that we need to multiply the given expression by the third root of seven squared divided by itself. By doing this we will end up with a numerator that is the third root of seven to the third power, or just 7.

The note to the left of Example 9 suggests that there is some arbitrary nature to the decision about rationalizing the numerator or the denominator of a fraction. It would be better to say that we decide to do one or the other depending upon the needs of the particular problem. Furthermore, from a historical computational perspective, we used to insist that answers be given with the denominator rationalized. Now, with the availablity of calculators, such a requirement does not make much sense.

Example 10 differs from the previous two examples in that it has a denominator with two terms. We wish to rationalize the denominator, which means, we want to change the form of the denominator so that it does not include a radical. To do this we use the fact that

(a-b)(a+b)=a²-b² We multiply the given expression by

divided by itself. The new denominator becomes ()() which then simplifies to 4-3.

The techniques of Examples 8 through 10 are important, and should be understood completely. At the same time, we can use the calculator to verify our work. All we need to do is to have the calculator evaluate the original expression and evaluate the "simplified" expression. The two answers must be essentially the same for us to have confidence that we have done the work correctly. The following screen captures from a TI-86 demonstrate the verification:

Example 8

Example 9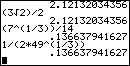

Example 10

In version 1 only

Note that the line directly below problem 13 on page 5 belongs directly below problem 14 on that page.

In the Exercises on page 5, try to do problems 17 through 20 by approximating values and then considering reasonable results.

Chapter 1, Section 1: Real and Complex Numbers

Not to be too picky, but with respect to the paragraph on page 7 related to Real Numbers:

In version 1 only

Cross out ", etc.,"
The numbers do not "lie on the number line", rather we can associate real numbers with points on the number line. We take a line, choose one point as 0 and another as 1, after which all other numbers can be associated with points on the line.

The number line should have had an arrow at each end.

In version 1 only

The last sentence of the paragraph should use the verb "has" as in "The set of real numbers has several important subsets."

In the paragraph on Natural Numbers, it is a bit dangerous to say "Sets with a last element are finite." We should say "Sets of natural numbers with a last element are finite."

In version 1 only

On page 8, the last sentence of the second paragraph should say "Cantor assigned the first transfinite number aleph-null,

, to the number of elements in the infinite set of natural numbers.

The cardinality of a set is the number of elements in the set. Therefore, we would say that the cardinality of the natural numbers is .

In version 1 only

On page 9, I find the explanation that

is countable to be next to impossible to follow. First, the discussion talks about making many different sets, one for each natural number, n=1, 2, 3, ..., but those sets are not shown in the final arrangement. In fact, in that arrangement the two sets,

and

are given but it is not clear that the natural numbers in the arrangement are "distinct in meaning" from the natural numbers associated with each small set. In addition, the negative values get included by the mere mention of "and their opposites".

In version 2 only

The explanation here is much better, but it still contains the problem of repeated rational values in the list. We could point out that since every natural number is also a rational number, it is clear that the cardinality of the rationals can not be less than the cardinality of the natural numbers. At the same time, as shown by the scheme in the book, and noting that rational values are repeated in the sequence, it is also clear that the cardinality of the natural numbers can not be less than the cardinality of the rational numbers. Therefore, the two sets must have the same cardinality.

Terminating and Repeating Decimals: Please look at the web pages

for additional material.

Chapter 1, Section 2: Inequalities and Absolute Value

On page 22, the number line should have an arrow on both ends. In fact, the number lines on pages 23, 24, and 25 should have arrows at both ends.

On page 23, the book introduces Combined Inequalities. students should pay a great deal of attention to this. In my experience, this concept has given rise to far too many student errors. It is essential that students recognize that

a < b < c is merely shorthand for a < b and b < c An interesting common error is to do a problem, end up with a solution such as 13 < x < 7 which is clearly wrong since, by transitivity, it would mean that 13 is less than 7 Generally, students have taken the "or" condition, 13 < x or x < 7 and have tried to condense it to a "combined inequality". In doing this, the students are in effect converting an "or" condition to an "and" condition. This is certain to give rise to an inappropriate result.

The presentation in the text of "open", "closed", and "half-open" intervals uses the parentheses and braces on the graph. Students should recognize that many texts (and tests) will use the open and filled dots to mark the endpoints of such intervals.

This is an important time to remember that the mathematical symbol (3,7) has at least three recognized meanings.

it could be the open interval from 3 to 7
it could be the complex number 3+7i [the TI-85 and TI-86 use this symbolism for complex numbers]
it could be the coordinates of a point on the Cartesian plane.

On pge 25, the second and third number lines each have a bold arrow that extends beyond the background number line. I believe that we should still be able to see that number line. I would prefer the second number line on the page appear as

and the third appear as

On page 26, the solution to Example 9 should read,

There is no largest member of the set. Any member of the set is smaller than a, since a is not in the interval. If we chhose any element of the set, call it b, then by the denseness property of the real numbers, there is another number between this member, b, and a. This means that no member of the set is largest. No matter what number we chhose fromt he set, there is always a larger number in the set.

The introduction of Union and Intersection, on page 27, is done without mentioning the concepts of set membership, , the negation of set membership, , subset, , proper subset, , and the empty set (also called the null set), symbolized either as or as { }. It is especially important to point out to students that

{} is NOT the empty set Rather that is the set that has one element, and that element is the empty set.

More information about sets can be found on the Notes on Sets page.

I would prefer that EXAMPLE 11 on page 27 be re-written as:

Find the intersection of {x|x3} and {x|x0} and write the solution in interval notation. (Note that the use of "and" implies intersection.)

Then follow that problem with

EXAMPLE 11a: When we have a set such as {x|x3 and x0} the use of "and" implies the intersection of the separate conditions. Find {x|x3 and x0} and write the solution in interval notation.

I would prefer that EXAMPLE 12 on page 27 be re-written as:

Find the union of {x|x0} or {x|x1} and write the solution in interval notation. (Note that the use of "or" implies union.)

Then follow that problem with

EXAMPLE 12a: When we have a set such as {x|x0 or x1} the use of "or" implies the union of the separate conditions. Find {x|x0 or x1} and write the solution in interval notation.

We need to point out that the solution to Example 13 could be written in other forms, one of which would be

(-3,12)(-124,5]

The properties of inequalities on page 28 can be given names. The first is the "Addition property of inequality", the second is the "Multiplication by a positive value property of inequality", and the third is the "Multiplicaiton by a negative value property of inequality".

The graph for example 14 on page 29 may not be so obvious to students. Look at the Example 14 page to see how that graph was developed. (TI-89 users can look at the TI-89 Example 14 page.) One important concept here is that we did not graph the problem

5x + 2 < x - 6 but rather we were forced by the calculator to graph two separate functions, y(x)=5x + 2 and y(x) = x - 6 and then to find all x-values where the first is below the second. This, in turn, means that we have to introduce the concept of "functions" here so that we can use them with the calculator. Unfortunately, the textbook will not cover the concept of "functions" until page 47.

It might have been nice to be able to graph the original problem

5x + 2 < x - 6 more directly. We can do this on the TI-86 (and on the TI-85) by observing that these calculators represent the value of "TRUE" with the number 1 and the value "FALSE" with the number 0. Unfortunately, the TI-89 does not use this scheme. In order to accomplish graphs similar to the ones presented below on the TI-89 we will need to introduce a special function. The function and the steps for using it are given at the end of the TI-89 Example 14 page. Therefore, instead of creating functions as we did on the Example 14 page, we could actually graph the function y(x)=5x+2<x-6 on the calculator. For each value of x where the inequality is true, the calculator will graph the value 1. For each value of x where the inequality is false, the calculator will graph the value 0. The y(x)= screen on a TI-86 for this appears as

(where the "<" sign is found in the TEST menu) and the resulting graph, with the WINDOW settings determined by ZSTD, appears as

Although we can see where the calculator has graphed the value of TRUE, that is, the value 1, we can not see where it has graphed the value False, that is, the value 0, because 0 lies on top of the x-axis. We can use a little trick to better enable us to see these two values, TRUE and FALSE. We do this by multiplying the original exression by 5 and then subtracting 2. The new function definition is

and the resulting graph is

ABSOLUTE VALUE:
I have created a separate page for a different approach to solving absolute value problems. That page includes both an alternative definition and numerous examples of applying that definition as a means tosolving absolute value problems.

On page 31, for Example 19, the TI-86 solution has been augemented, incorrectly, to identify the right-side intersection point as (5/2,3). This should be (5,3). Students should note that the graph was the result of defining two functions as

y1=abs(x-2)
y2=3

On page 37, Example 28, the Solution contains "see Example 28". This should probably be "See Example 26".

Chapter 1, Section 3: Relations and Functions

In version 1 only

Page 43, first paragraph, third sentence: "Graphs make it possible to quickly draw conclusions from tables of data." I prefer to say "Graphs make it possible to quickly draw conclusions about the relationship between values that are in tables of data."

The graph in the middle of the page should have arrows at both ends of the axes. The sentence below the graph should be "The coordinate system, as shown above, consists of two perpendicaular lines whose point of intersection is called the origin. It is at this point of intersection that we place the zero, 0, of the horizontal number line, and the zero, 0, of the vertical number line."

The next paragraph should start with "An ordered pair of real numbers, (a,b), is graphed by starting at the origin and moving horizontally to the point that is a units from the origin, then moving vertically a distance corresponding to b units from the origin on the vertical axis." And, the paragraph should end with "Since the origin is zero horizontal and vertical units away from itself, the coordinate of the origin is (0,0)."

In version 1 only

Page 44. It is nice to have the clean clear calculator driven picture for the solution to example 1. However, we are not given the scales of the graph. We can only assume that the "tic marks" represent 1 unit on each of the axes. A note that indicated that the graph was from a TI-86 with Zdecimal settings would take care of this.

In version 1 only

The last paragraph on page 44 starts with "Since a relation can be defined as a set of ordered pairs,..." In fact, a relation is a set of ordered pairs. We have no other interpretation of it.

In version 1 only

Page 47, top, solutions b) and c) should not use the

symbol. For solution b) the Domain is not an element of [–3,4], the Domain is [–3,4]. We could say that if x

D then x

[–3,4].

In version 1 only

There is a problem that we get into when we allow an element of a set to be listed more than once in the set. For example, the set A={1,2,3,2,3,4} is equal to the set B={1,2,3,4}. After all, for any x

A we have x

B, and for any x

B we have x

A. Generally, we try to not list an element of a set more than once. However, if we recogize that it is possible to do so, then we need to modify the definition of a function ever so slightly. We should say "A relation in which no two distinct ordered pairs have the same first coordinate, abscissa, is called a function. That is, in a function each domian element appears with exactly one range element. However, the range elements need not appear with only one domain element."

In version 1 only

Page 47 at the bottom, the word function is inserted in error in the second to last sentence. The bottom paragraph should read "A function in which no two distinct ordered pairs have the same second coordinate, ordinate, is called one–to–one. That is, in a one–to–one function each range element appears with only one domain element."

In version 1 only

Page 48, the picture at the bottom of the page has two points that are given labels. The labels are (x,y₁) and (x,y₂), but they should be (x₁,y₁) and (x₁,y₂).

Page 50. I would like to make a small change to the first sentence on the page, and then add a few more sentences. As a result the first paragraph would be:

We know that a function has been defined as a relation where no two ordered pairs have the same first coordinate. Any relation that meets that criterion is a function. That allows us to define some strange functions, most of which are not of much interest to us. Interesting functions are those that have an external "rule" or a "method of computation" that assigns a range value to each domain value. In particular, we would like to be able to express such a rule in words or via some algebraic notation. The only things that we require are that the rule tells us exactly how to associate a range element to each domain element, and that such an association is valid for every domain value.

Page 51. Here the text introduces the function notation f(x)=2x+1. I prefer to say that if f is a function then f must be a relation (a set of ordered pairs) that meets our criteria (no domain element is associated with more than one range element), and there may be a convenient "rule" that we can use to identify the ordered pairs that make up the function f. For example, we might write

f={ (x,y) | y = 2x + 1 } This identifies f as a set of ordered pairs, and it gives us a rule for determining a single range value for any given domain value. We abbreviate this notation in two different ways. First, we often dismiss the set notation and just write y = 2x + 1 Second, because the rule, in this case 2x+1, predicts the range value based upon a given domain value, we use the abbreviation f(x) = 2x + 1 to mean that we are defining a function, f, by the rule that states "for any domain value x we determine the range value by evaluation the expression 2x+1". In fact, we read f(x) = 2x + 1 as f of x is defined to be 2x+1 Later on we will continue this confussion of abbreviations by talking about the ordered pair (x,f(x)). There are times that the function notation f(x) = 2x + 1 is extremely convenient.

In version 1 only

Page 52, middle of the page, as part of the solution, part a), there should be a second line that expands the given f(3a)=(3a)²–2(3a)+3 into = 9a²–6a+3

Chapter 1, Section 4: Algebra and the Composition of Functions

In version 1 only

Page 60, Example 4, Solution: I understand the intended meaning of the solution when it is written as D _f = {x|x–4 or 3/2} but it would be much better to write this as as D _f = {x|x–4 and x3/2}

In version 1 only

Page 63, at the bottom, there is an overtyping and the definition of f(x) is hard to make out. It should read as "For example if f(x) = x² – 1 and g(x) = 2x – 3

Chapter 1, Section 5: Symmetry, Increasing and Decreasing Functions

(A small note: the title of the section is different from that given in the Table of Contents).

In version 2 only

The graphs on page 74 are now missing the arrows on all of the axes.

In version 2 only

Example 6, on pages 78 and 79, refers to a line L. However, that line is not marked on the graph (at the top of page 79). The horizontal line (the x-axis) is meant to be line L.

At the bottom of page 86, there is an image, taken from a calculator, of the graph of the functions discussed in the text. It is important for students to note the distortion in the graph due to the WINDOW (RANGE) settings of the calculator. In particular, the line y=x does not appear to be at the appropriate 45° angle.