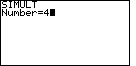
 and
and  , but for the TI-86
we start with
, but for the TI-86
we start with  and
and  . On either calculator this selects the "SIMULT" function.
The calculator responds with a request for the
value of "Number" as shown in Figure 1. The SIMULT function expects to have exactly the
same number of equations as we have variables. For our problem, we have 4 variables
and 4 equations. Therefore we respond with the
. On either calculator this selects the "SIMULT" function.
The calculator responds with a request for the
value of "Number" as shown in Figure 1. The SIMULT function expects to have exactly the
same number of equations as we have variables. For our problem, we have 4 variables
and 4 equations. Therefore we respond with the  key to complete
Figure 1.
key to complete
Figure 1.
 key.
That will cause the display to change to Figure 2. Notice in Figure 2 that the
calculator is requesting values for each of the coefficients and constants
that we have in the general standard form for our first equation. The first
subscript on each of the "a's" and the subscript on the "b" indicates that we
are looking at values for the first equation.
key.
That will cause the display to change to Figure 2. Notice in Figure 2 that the
calculator is requesting values for each of the coefficients and constants
that we have in the general standard form for our first equation. The first
subscript on each of the "a's" and the subscript on the "b" indicates that we
are looking at values for the first equation. 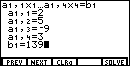











 . After pressing
those keys the screen should appear as in Figure 3.
. After pressing
those keys the screen should appear as in Figure 3. 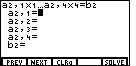
 key. Notice that the display is now asking for values
for the second equation, as indicated by the subscripts.
key. Notice that the display is now asking for values
for the second equation, as indicated by the subscripts. 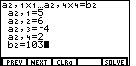










 and
and  to produce the display shown in Figure 5.
to produce the display shown in Figure 5.
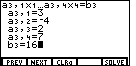
 key. Notice that the display is now asking for values
for the third equation, as indicated by the subscripts.
key. Notice that the display is now asking for values
for the third equation, as indicated by the subscripts.
The values for the coefficients and constant in the third equation are
3, -4, 2, 7, and 16. We press









 and
and  to produce the display shown in Figure 6.
to produce the display shown in Figure 6.
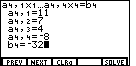
 key. Notice that the display is now asking for values
for the fourth equation, as indicated by the subscripts.
key. Notice that the display is now asking for values
for the fourth equation, as indicated by the subscripts.
The values for the coefficients and constant in the fourth equation are
11, 7, 4, -8, and -32. We press











 and
and  to produce the display shown in Figure 7.
to produce the display shown in Figure 7.
 key to select the "SOLVE" option from the
menu. The calculator responds with the solution shown in Figure 8.
key to select the "SOLVE" option from the
menu. The calculator responds with the solution shown in Figure 8.
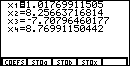
This is the solution to the equations that we have entered via the coefficients and the constants. Unfortunately, these are the wrong values for our original problem. [This being a problem for a math class, we expect that the answers will be fairly "nice", most likely integer values, or at worst common fractions.] These values do not make the original first equation work. 2*1.0169911505 + 5*8.25663716814 + -4*(-7.70796460177 + 3*8.76991150442 is 138.998... or, essentially, 139. Our original first equation was
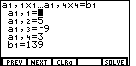
 key to select the "COEFS" option. This returns us to the data entry screen for
the first equation, as shown in Figure 9, Note that the blinking cursor is covering the
value 2 assigned to the first coefficient.
key to select the "COEFS" option. This returns us to the data entry screen for
the first equation, as shown in Figure 9, Note that the blinking cursor is covering the
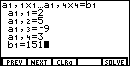
value 2 assigned to the first coefficient.An examination of this list of coefficients and the constant reveals our error. The value for b1 should have been 151, not 139. This is the error introduced back in Figure 3.
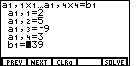



 to change the display to correspond to Figure 10.
to change the display to correspond to Figure 10.


 ,
producing the putput in Figure 11.
,
producing the putput in Figure 11.
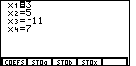
 key to select the "SOLVE" option from the
menu. The calculator responds with the solution shown in Figure 12. Thus,
there is a solution to all four equations when
x1 or x is 3, x2 or y is 5,
x3 or z is -11, and
x4 or w is 7.
key to select the "SOLVE" option from the
menu. The calculator responds with the solution shown in Figure 12. Thus,
there is a solution to all four equations when
x1 or x is 3, x2 or y is 5,
x3 or z is -11, and
x4 or w is 7. , while on the TI-86 it is
, while on the TI-86 it is
 . To save some space, and to ignore this difference, the numeric keys
(the gray ones) have been changed here to only show the key
face, as in
. To save some space, and to ignore this difference, the numeric keys
(the gray ones) have been changed here to only show the key
face, as in  key will be shown as
key will be shown as