We are looking for the values of the variables that make all four equations true.
[Remember that
these are linear equations in four variables. In the earlier
example of two variables in two equations, we could associate the problem with
lines on in a Cartesian plane where each equation
represents a line. In the 3 equation 3 variable situation
we could associate each equation with a plane in Cartesian space.
For 4 equations and 4 variables we no longer have the luxury of a
physical model. Nonetheless the observations of the earlier
situations hold true. There are an infinite number of 4 values (one for each
of x, y, z, and w) that make each equation true.
In the problem given above, there is exactly one set of 4 values that
make all four equations true. We need to find that set of 4 values, for
x, y, z, and w, that solve all four equations.]
Before we actually start using the calculator, remember that the calculator will be using
a general form for each of the equations, expecting the equations to have the variables
is the same order. The earlier pages had much longer explanations of this. Here we
will just point out that the calculator will use
Now, onto the problem on the calculator.
Figure 1
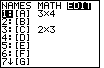
| Press the  key to openthe matrix menu, and
then key to openthe matrix menu, and
then   to shift
the menu selection to EDIT.
The calculator used here shows that two matrices have been defined previously,
[A] and [C]. Matrix [A] is a 3x4 matrix (3 rows and 4 columns)
and [C] is a 2x3 matrix. For our problem we will
need to use a 4x5 matrix to hold the coefficients and the constants.
We will use [C] for our work on this page. We select [C]
by pressing the to shift
the menu selection to EDIT.
The calculator used here shows that two matrices have been defined previously,
[A] and [C]. Matrix [A] is a 3x4 matrix (3 rows and 4 columns)
and [C] is a 2x3 matrix. For our problem we will
need to use a 4x5 matrix to hold the coefficients and the constants.
We will use [C] for our work on this page. We select [C]
by pressing the  key. This shifts the calcualtor to
Figure 2. key. This shifts the calcualtor to
Figure 2.
|
Figure 2

| The blinking cursor is on the "2" in the 2x3 designation of the
size of the matrix. We want a matrix with 4 rows. Therefore,
we press   keys to change the number of
of rows.
The cursor will jump to the "3" in what was 2x3, representing the number of
columns. We will need 5 columns. Therefore, press the keys to change the number of
of rows.
The cursor will jump to the "3" in what was 2x3, representing the number of
columns. We will need 5 columns. Therefore, press the
 key to set the number of
of columns to the desired 5.
The result is shown in Figure 3. key to set the number of
of columns to the desired 5.
The result is shown in Figure 3.
|
Figure 3

| Figure 3 shows the effect of the change made so far.
In particular, the matrix now has
four rows. The two new rows are filled with 0's.
At the same time, the matrix still has 3 columns. Note
that we have not pressed the ENTER key yet. The cursor is
still in the column field of the matrix size
at the top of the screen. Once we press  the calculator will add the extra two columns to the right side of the matrix,
as shown in Figure 4.
the calculator will add the extra two columns to the right side of the matrix,
as shown in Figure 4.
|
Figure 4
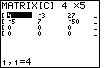
| At this point the matrix has been resized. Now we need to enter the
desired values into the matrix in the desired places.
The cursor is at row 1 column 1 where the old value is 4.
However, we want the calculator to hold the matrix
| 2 | 5 | – 9 | 3 | 151 |
| 5 | 6 | – 4 | 2 | 103 |
| 3 | – 4 | 2 | 7 | 16 |
| 11 | 7 | 4 | – 8 | – 32 |
|
Figure 5
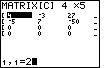
| Therefore, press  to change the value stored
in row 1 column 1. The display changes to that shown in Figure 5.
Note that we have not finished entering the new value.
As such, the value in the actual matrix is still 4. We can
press the to change the value stored
in row 1 column 1. The display changes to that shown in Figure 5.
Note that we have not finished entering the new value.
As such, the value in the actual matrix is still 4. We can
press the  key to accept the value. key to accept the value.
|
Figure 6

| Figure 6 shows the screen after we have entered
  for row 1 column
2 and for row 1 column
2 and   to start the process to change the element at row 1 column 3.
to start the process to change the element at row 1 column 3.
We can press  to move to Figure 7. to move to Figure 7.
|
Figure 7
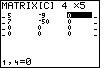
| Our value for row 1 column 3 has been accepted. The calculator
has shifted to the element at row 1 column 4. The current value is 0.
|
Figure 8
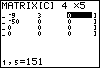
| The next keystrokes are  
 . .
Press  to
accept the value 151 for row 1 column 5 and move to the next screen. to
accept the value 151 for row 1 column 5 and move to the next screen.
|
Figure 9

| The calculator shifts to the element at row 2 column 1.
the number in that cell is — 5, left over from the
earlier matrix [C]. We continue to enter values for the rest of the cells
of the matrix.
|
Figure 10
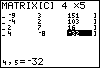
| Figure 10 shows the screen after we have entered all of the
values for our desired matrix. Note that the calculator is still
at row 4 column 5. We can take this opportunity to review the elements
of the matrix and to compare them to the desired matrix. In Figure 10 we can see
only the final three columns of the matrix. After reviwing those twelvve values, we
can press the  key four times to
move the highlight back to row 5 column 1, as shown in Figure 11. key four times to
move the highlight back to row 5 column 1, as shown in Figure 11.
|
Figure 11

| Now we can compare the values in the leftmost three columns with the
desired matrix. If we find an incorrect value then we
can use the cursor keys to move the highlight to that element.
Then we can enter a new value for that element.
Once we are satisfied that the
values are correct, we can get out of the matrix editor by
pressing the key
sequence   .
This will take us back to the main screen, shown, for this
calcualtor, in Figure 12. .
This will take us back to the main screen, shown, for this
calcualtor, in Figure 12.
|
Figure 12

| The calculator used in this example had a blank main screen.
In order to try to solve our problem we want to create the command
rref([C]). We can find the rref( command in the matrix menu.
|
Figure 13

| Press  to open
the matrix menu, and to open
the matrix menu, and  to shift the highlight to the
MATH menu. Then use the to shift the highlight to the
MATH menu. Then use the  to move down the
menu to find the rref( item. to move down the
menu to find the rref( item.
|
Figure 14

| Press  to select that item and paste it onto the
screen, as shown in Figure 14. to select that item and paste it onto the
screen, as shown in Figure 14.
|
Figure 15

| Return to the matrix menu with the  key
in order to select the name of the matrix, [C]
via the key
in order to select the name of the matrix, [C]
via the  key. key.
|
Figure 16

| Then complete the command with
  . The
result is shown in Figure 16. We read this display by converting it back to equations . The
result is shown in Figure 16. We read this display by converting it back to equations
1x + 0y + 0z + 0w = 3
0x + 1y + 0z + 0w = 5
0x + 0y + 1z + 0w = – 11
0x + 0y + 0z + 1w = 7
|
These give us x=3, y=5, z=– 11, and w=7.
|
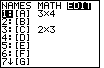
 key to openthe matrix menu, and
then
key to openthe matrix menu, and
then 
 to shift
the menu selection to EDIT.
The calculator used here shows that two matrices have been defined previously,
[A] and [C]. Matrix [A] is a 3x4 matrix (3 rows and 4 columns)
and [C] is a 2x3 matrix. For our problem we will
need to use a 4x5 matrix to hold the coefficients and the constants.
We will use [C] for our work on this page. We select [C]
by pressing the
to shift
the menu selection to EDIT.
The calculator used here shows that two matrices have been defined previously,
[A] and [C]. Matrix [A] is a 3x4 matrix (3 rows and 4 columns)
and [C] is a 2x3 matrix. For our problem we will
need to use a 4x5 matrix to hold the coefficients and the constants.
We will use [C] for our work on this page. We select [C]
by pressing the  key. This shifts the calcualtor to
Figure 2.
key. This shifts the calcualtor to
Figure 2.


 keys to change the number of
of rows.
The cursor will jump to the "3" in what was 2x3, representing the number of
columns. We will need 5 columns. Therefore, press the
keys to change the number of
of rows.
The cursor will jump to the "3" in what was 2x3, representing the number of
columns. We will need 5 columns. Therefore, press the
 key to set the number of
of columns to the desired 5.
The result is shown in Figure 3.
key to set the number of
of columns to the desired 5.
The result is shown in Figure 3.

 the calculator will add the extra two columns to the right side of the matrix,
as shown in Figure 4.
the calculator will add the extra two columns to the right side of the matrix,
as shown in Figure 4.
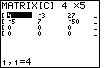
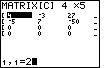
 to change the value stored
in row 1 column 1. The display changes to that shown in Figure 5.
Note that we have not finished entering the new value.
As such, the value in the actual matrix is still 4. We can
press the
to change the value stored
in row 1 column 1. The display changes to that shown in Figure 5.
Note that we have not finished entering the new value.
As such, the value in the actual matrix is still 4. We can
press the  key to accept the value.
key to accept the value.


 for row 1 column
2 and
for row 1 column
2 and 
 to start the process to change the element at row 1 column 3.
to start the process to change the element at row 1 column 3.
 to move to Figure 7.
to move to Figure 7.
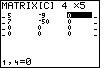




 .
.  to
accept the value 151 for row 1 column 5 and move to the next screen.
to
accept the value 151 for row 1 column 5 and move to the next screen.

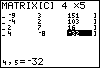
 key four times to
move the highlight back to row 5 column 1, as shown in Figure 11.
key four times to
move the highlight back to row 5 column 1, as shown in Figure 11.


 .
This will take us back to the main screen, shown, for this
calcualtor, in Figure 12.
.
This will take us back to the main screen, shown, for this
calcualtor, in Figure 12.


 to open
the matrix menu, and
to open
the matrix menu, and  to shift the highlight to the
MATH menu. Then use the
to shift the highlight to the
MATH menu. Then use the  to move down the
menu to find the rref( item.
to move down the
menu to find the rref( item.

 to select that item and paste it onto the
screen, as shown in Figure 14.
to select that item and paste it onto the
screen, as shown in Figure 14.

 key
in order to select the name of the matrix, [C]
via the
key
in order to select the name of the matrix, [C]
via the  key.
key.

 . The
result is shown in Figure 16. We read this display by converting it back to equations
. The
result is shown in Figure 16. We read this display by converting it back to equations
 key.
The text below will be done from the perspective of the TI-83. That is, all
reference to the MATRIX key will be demonstrated via the
key.
The text below will be done from the perspective of the TI-83. That is, all
reference to the MATRIX key will be demonstrated via the
 .
In addition, the
.
In addition, the  and the
and the  , again to save space.
, again to save space.