We are looking for the values of the variables that make all four equations true.
Figure 1
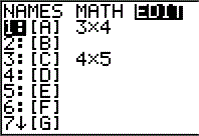
| Open the matrix menu and move to the editor. We will use [A]
for this problem.
|
Figure 2
| [A] does not have the correct dimensions for the current problem. We need
to change those dimensions to be 4x5 to hold
the four equations each with four coefficients and a constant. Not seen in Figure 2
is the blinking cursor, although it was over the initial 3 at the top of the screen.
|
Figure 3

| Pressing   
 changes the dimensions and moves us to the
first element of the matrix. Note that there is a new row at the bottom of
the matrix, prefilled with 0 values. changes the dimensions and moves us to the
first element of the matrix. Note that there is a new row at the bottom of
the matrix, prefilled with 0 values.
|
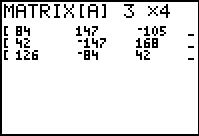
Figure 4

| In Figure 4 all of the coefficient and constant values have been entered into the matrix.
Only the last three columns of the matrix are visible. We can use these to verify the entry
of correct values from the problem.
|
Figure 5

| To check the values in the left columns of the matrix we use the
 key to move the display, as shown in
Figure 5. key to move the display, as shown in
Figure 5.
|
Figure 6
| Use   to
exit the matrix editor and return to the main screen. to
exit the matrix editor and return to the main screen.
|
Figure 7
| Use   to recall the
previous command. That is not the one we want, so we
use to recall the
previous command. That is not the one we want, so we
use   again to
recall the command before that. again to
recall the command before that.
|
Figure 8
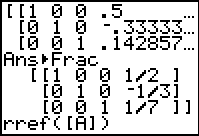
| Now that we have the right command, we might as well append the
command to convert the answer to fractional form just in case we need it.
Press  to get to the MATH menu. to get to the MATH menu.
|
Figure 9

| Press  to select the highlighted command. to select the highlighted command.
|
Figure 10
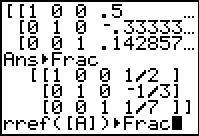
| With the command in place, press  to perform the
command. to perform the
command.
|
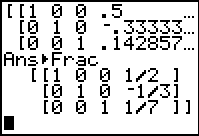
Figure 11
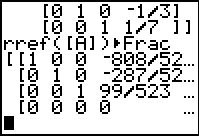
| The answer, or at least the left part of the answer matrix, appears in Figure 11. The bottom row gives
us cause for concern. All four of the values there are 0. We need to inspect the
right portion of the answer to get the resst of the information.
|
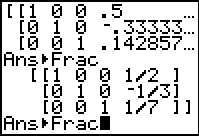
Figure 12

| Use the  key to see the right portion, as in FIgure 12.
Here we see that we have 0 values all the way across the last row.
If we translate that last row back into the equation form
we would have
0x + 0y + 0z +0w = 0
Therefore, we conclude that there are an infinite number of solutions to this
system of linear equations. key to see the right portion, as in FIgure 12.
Here we see that we have 0 values all the way across the last row.
If we translate that last row back into the equation form
we would have
0x + 0y + 0z +0w = 0
Therefore, we conclude that there are an infinite number of solutions to this
system of linear equations.
|
The 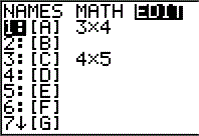





 changes the dimensions and moves us to the
first element of the matrix. Note that there is a new row at the bottom of
the matrix, prefilled with 0 values.
changes the dimensions and moves us to the
first element of the matrix. Note that there is a new row at the bottom of
the matrix, prefilled with 0 values.


 key to move the display, as shown in
Figure 5.
key to move the display, as shown in
Figure 5.


 to
exit the matrix editor and return to the main screen.
to
exit the matrix editor and return to the main screen.


 to recall the
previous command. That is not the one we want, so we
use
to recall the
previous command. That is not the one we want, so we
use 
 again to
recall the command before that.
again to
recall the command before that.

 to get to the MATH menu.
to get to the MATH menu.

 to select the highlighted command.
to select the highlighted command.

 to perform the
command.
to perform the
command.


 key to see the right portion, as in FIgure 12.
Here we see that we have 0 values all the way across the last row.
If we translate that last row back into the equation form
we would have
key to see the right portion, as in FIgure 12.
Here we see that we have 0 values all the way across the last row.
If we translate that last row back into the equation form
we would have  key, whereas on the TI-83 Plus
requires 2 keys to achieve the same result, namely, the
key, whereas on the TI-83 Plus
requires 2 keys to achieve the same result, namely, the

 key.
The text below will be done from the perspective of the TI-83. That is, all
reference to the MATRIX key will be demonstrated via the
key.
The text below will be done from the perspective of the TI-83. That is, all
reference to the MATRIX key will be demonstrated via the
 .
In addition, the
.
In addition, the