Figure 1
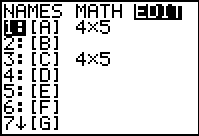
| Open the matrix menu and move to the editor. We will use [A]
for this problem.
|
Figure 2
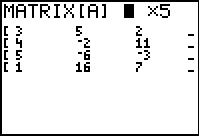
| [A] does not have the correct dimensions for the current problem. We need
to change those dimensions to be 3x2 to hold
the two equations each with two coefficients and a constant. Not seen in Figure 2
is the four under the blinking cursor, although we know it is four since there are
four rows in the matrix.
|
Figure 3

| For Figure 3 we have changed the dimensions of the matrix and we have entered all of the values
to represent our two equations.
|
Figure 4
| Use   to
exit the matrix editor and return to the main screen. to
exit the matrix editor and return to the main screen.
|
Figure 5
| Use   to recall the
previous command. to recall the
previous command.
|
Figure 6
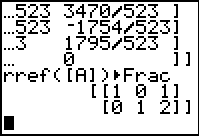
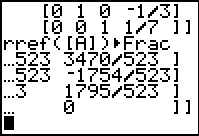
| Press  to perform the
command. The response is shown in Figure 6. From this we
see that for the two equations
-2x + y = 0 to perform the
command. The response is shown in Figure 6. From this we
see that for the two equations
-2x + y = 0
4x - 9y = -14
have become
1x + 0y = 1
0x + 1y = 2
That is, the two lines intersect at the point (1,2). Now we will
look at the third equation along with the second equation.
|
Figure 7

| To do this we just need to return to the matrix editor
and change a row of values. This has been done in Figure 7.
|
Figure 8
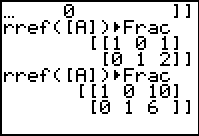
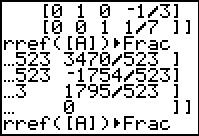
| To solve that system of equations, we return to the main menu and recall the previous command
and then perform it. The result is shown in Figure 8.
the two equations
1x + 3y = 28
4x - 9y = -14
have become
1x + 0y = 10
0x + 1y = 6
That is, the two lines intersect at the point (10,6). This
is a different point of intersection than we had witht he first two equations.
Therefore, the three equations cannot possibly intersect in one point.
|
Figure 9

| So far we have looked at the system of the first and second equations and
the system of the third and second equations. From that inspection we know that there
is not a single point where they all intesect.
It is not necessary to find out where the first and third equations intersect, but it cannot hurt.
We return to the matrix editor, replace the second equation values with those
of the first equation. This change is shown in Figure 9.
|
Figure 10

| Returning to the main screen, recalling the command and performing it
shows that the first and third equations intersect at yet a different point, (4,8).
|
Figure 11
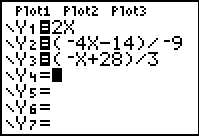
| Especially in this case, it is instructive to go ahead and just graph the
three equations. Moving to the Y= screen, we have entered the
three equations into the calculator. Note that the "style"
of this entry is one of convenience rather than to duplicate the slope-intercept form of the
equation. The calculator does not care if the equation is in the formal y=mx+b format.
|
Figure 12
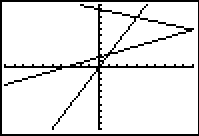
| Recognizing that the points of intersection are (1,2), (10,6), and
(4,8), we know that we will get a good graph using the Zoom Standard setting.
This has been done in Figure 12. There we can see that the three lines intersect pairwise
in the expected points.
|
Figure 13
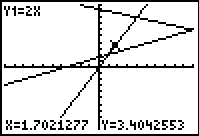
| This figure, and the two subsequent figures merely provide the trace information
for the three equations on the graph.
We use the  key to move from equation to
equation in the graphs. key to move from equation to
equation in the graphs.
|
Figure 14

|
|
Figure 15
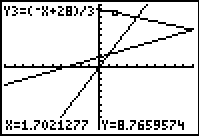
|
|
The 




 to
exit the matrix editor and return to the main screen.
to
exit the matrix editor and return to the main screen.


 to recall the
previous command.
to recall the
previous command.

 to perform the
command. The response is shown in Figure 6. From this we
see that for the two equations
to perform the
command. The response is shown in Figure 6. From this we
see that for the two equations 






 key to move from equation to
equation in the graphs.
key to move from equation to
equation in the graphs.

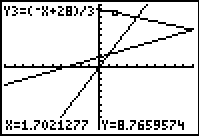
 key, whereas on the TI-83 Plus
requires 2 keys to achieve the same result, namely, the
key, whereas on the TI-83 Plus
requires 2 keys to achieve the same result, namely, the

 key.
The text below will be done from the perspective of the TI-83. That is, all
reference to the MATRIX key will be demonstrated via the
key.
The text below will be done from the perspective of the TI-83. That is, all
reference to the MATRIX key will be demonstrated via the
 .
In addition, the
.
In addition, the