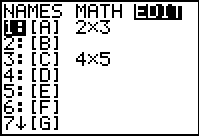



However, as in the previous example, it might be interesting to see the solution to the first and third equations.


 key, whereas on the TI-83 Plus
requires 2 keys to achieve the same result, namely, the
key, whereas on the TI-83 Plus
requires 2 keys to achieve the same result, namely, the

 key.
The text below will be done from the perspective of the TI-83. That is, all
reference to the MATRIX key will be demonstrated via the
key.
The text below will be done from the perspective of the TI-83. That is, all
reference to the MATRIX key will be demonstrated via the
 key. If the user has a TI-83 Plus then the key strokes should be
key. If the user has a TI-83 Plus then the key strokes should be

 .
To save some space, and to ignore this difference, the numeric keys
(the gray ones) have been changed in some places to show the key
face, as in
.
To save some space, and to ignore this difference, the numeric keys
(the gray ones) have been changed in some places to show the key
face, as in  .
In addition, the
.
In addition, the  key may be shown as
key may be shown as  and the
and the  key may be shown as
key may be shown as  , again to save space.
, again to save space.
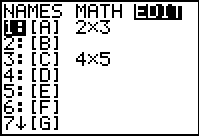
| Move to the EDIT tab of the MATRIX menu. Again, we will use matrix [A] for this problem. |

| Matrix [A] has the correct dimensions for solving a system of two equations in two variables, namely 2 rows and 3 columns. For Figure 2 we have gone forward and entered the coefficients and constants from the first two equations. |

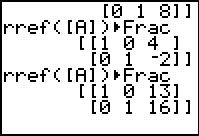
| In Figure 3 we have quit the matrix editor, recalled the command that we want to use, and performed the command. The resulting matrix yields the solution x=4 and y=–2. |

| Having found a point of intersection for the first two equations, we can return to the matrix editor and change the first row to hold the values from the third equation. The changed matrix, shown in Figure 4, represents the third and second equations. |

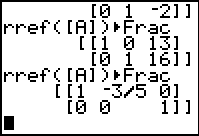
| In Figure 5 we have quit the matrix editor, recalled the command that we want to use,
and performed the command. The resulting matrix yields the solution
x=13 and y=16. These values, being different from the
coordinates of the solution to the first two equations, are enough to
determine that there is no unique solution to the three equations.
However, as in the previous example, it might be interesting to see the solution to the first and third equations. |

| To do this we return to the matrix editor where we replace the second row with the coefficients and constant from the first equation. |

| In Figure 7 we have quit the matrix editor, recalled the command that we want to use,
and performed the command. The resulting matrix indicates that there is no solution to
this pair of equalities. The second row now represents the impossible equation
|

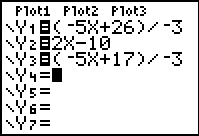
| In Figure 8 we have the Y= screen where we have entered all three equations. |

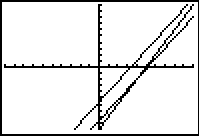
| An initial graph of the three equations, in the ZOOM Standard settings, shows the two parallel lines and a line cutting across them (a transverse line). |

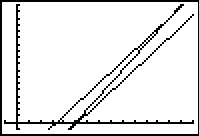
| Knowing the two points of intersection we can adjust, as shown in Figure&10, the WINDOW settings to show both points. |

| This is merely the new graph, in the new WINDOW settings, showing the two parallel lines (equations 1 and 3) and the transverse line (equation 2). |
©Roger M. Palay
Saline, MI 48176
November, 2010