Figure 1
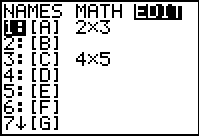
| Here we are in the MATRIX menu and we have moved to highlight
the EDIT tab. We will use matrix [A] for this problem. The current
dimensions for [A], 2 rows and 3 columns, will need to be changed.
|
Figure 2

| In Figure 2 the dimensions of [A] have been changed. Note the added row of values
at the bottom of the matrix.
|
Figure 3

| For FIgure 3 we have entered all of the coefficients and constants for the three equations
that we are using. Note that we see the right side of the matrix in Figure 3.
|
Figure 4

| We can use the  key to move the display
so that we can verify the values in the other column of the matrix. key to move the display
so that we can verify the values in the other column of the matrix.
|
Figure 5
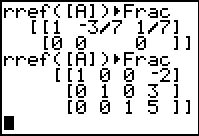
| We quit the matrix editor, recall the rref command, and
execute it. The result, shown in Figure 5 gives us the transformed equations
that indicate that the solution is x=–2, y=3,
and z=5. Knowing that we have a solution for the first three of our equations
means that we can test those values on the fourth equation:
7x + 3y + 2z = 5
7*–2 + 3*3 + 2*5 ?= 5
–14 + 9 + 10 ?= 5
5 = 5
Therefore, the values x=–2, y=3,
and z=5 not only satisfy the first three equations they also satisfy the fourth.
That makes those values be the solution of the system of four linear equations.
|
Figure 6

| Of course, we could throw the fourth equation into the matrix along with two of the other
equations and use rref to solve that system. That is what we have done in Figure 6, replacing the first
equation with the values of the fourth.
|
Figure 7

| Returning to the main screen, recalling and running the comand, produces the
matrix shown in Figure 7. Again, we have the same
solution, but this time for the fourth, second, and third equations.
|
Figure 8
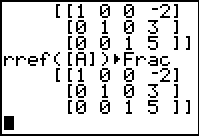
| Returning to the main screen and performing the command again gives us the same unique solution.
|
The 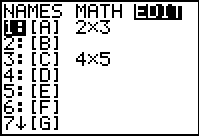



 key to move the display
so that we can verify the values in the other column of the matrix.
key to move the display
so that we can verify the values in the other column of the matrix.




 key, whereas on the TI-83 Plus
requires 2 keys to achieve the same result, namely, the
key, whereas on the TI-83 Plus
requires 2 keys to achieve the same result, namely, the

 key.
The text below will be done from the perspective of the TI-83. That is, all
reference to the MATRIX key will be demonstrated via the
key.
The text below will be done from the perspective of the TI-83. That is, all
reference to the MATRIX key will be demonstrated via the
 .
In addition, the
.
In addition, the  key may be shown as
key may be shown as  and the
and the  , again to save space.
, again to save space.