TI-83: Complex 4 equation 3 variable situation, without a solution

The main page for solving systems of linear equations on the TI-83 and TI-83 Plus.
The previous example page covers a Complex 4 equation 3 variable situation, where there is a solution.

WARNING: The TI-83 and TI-83 Plus are almost identical in terms of the material presented here. The major difference is the labels that are on certain keys. The TI-83 has a

key, whereas on the TI-83 Plus requires 2 keys to achieve the same result, namely, the

key. The text below will be done from the perspective of the TI-83. That is, all reference to the MATRIX key will be demonstrated via the

key. If the user has a TI-83 Plus then the key strokes should be

. To save some space, and to ignore this difference, the numeric keys (the gray ones) have been changed in some places to show the key face, as in

. In addition, the

key may be shown as

and the

key may be shown as

, again to save space.

The problem we will use on this page is 13x - 39y + 78z = 377
-10x - 51y + 48z = 7
-37x + 57y - 33z = -290
60x - 45y + 63z = 309 Similar to the previous examples, we have more equations than we have variables. In this example there are three variables, but we have 4 equations. Our use of the rref function has been in situations where the number of equations is equal to the number of variables. In a real sense, we have an extra equation here. If we only had three equations then we could use rref to find their point of intersection. Let us move ahead in that direction. At first we will restrict our analysis to the first three equations: 13x - 39y + 78z = 377
-10x - 51y + 48z = 7
-37x + 57y - 33z = -290

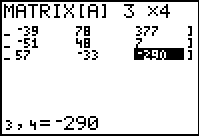
Figure 1	Figure 1 shows the right side of matrix [A] after we have entered the coefficients and constants for the three equations being considered.
Figure 2	This display merely shifts the display so that we can verify the values on the left side of the matrix.
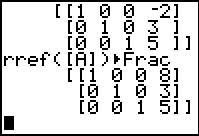
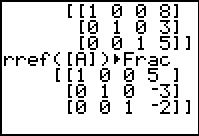
Figure 3	Here we returned to the main screen, recalled the command, and performed it. We read out the solution x=8, y=3, and z=5. As in previous examples, we have at least two ways to see if this solution, derived from the first three equations, is indeed a solution for all four equations. We could use these values in the fourth equation to see if this is also a solution to that equation: 60x - 45y + 63z = 309 608 - 453 +63*5 ?= 309 480 - 135 + 315 ?= 309 654 != 309 where we use the symbol "!=" to mean "not equal to". Thus, the solution to the first three equations does not satisfy the fourth and there is no solution for all four equations.
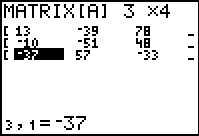
Figure 4	Of course, we could just replace the values of the first equation with those of the fourth in our matrix and use rref to solve that set of three equations. The matrix shown in Figure&4 shows the left side of the altered matrix.
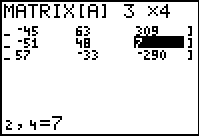
Figure 5	Here we see the right side of the altered matrix.
Figure 6	Finally, we recall and perform the command only to find that the fourth, second, and third equations have a solution at x=5, y=^–3, and z=^–2, a different point than we found for the first, second, and third equations. The conclusion is that the four equations do not have a point in common.

The main page for solving systems of linear equations on the TI-83 and TI-83 Plus.
The previous example page covers a Complex 4 equation 3 variable situation, where there is a solution.