|
Spoiler Alert: Although understanding probability
is essential to understanding inferential statistics, the
breadth and depth of the topic presented here
far exceeds that required for the inferential statistics
that will be presented in this course. However, the course syllabus,
and for the most part the syllabus for just about every college level
introductory statistics course, includes all of the probability
topics that will be presented here. Probability, as a subject matter, is quite different from statistics. Being different, this material may require different learning strategies. Be aware that we are changing directions here and that you may have to self-assess your own mastery of this material in a slightly different way. |
|
It is important to note that probability must be
between 0 and 1, inclusive. If you
are working on a problem and you compute the answer
to be a probability that is greater than 1 or less than 0 then
your answer is wrong.
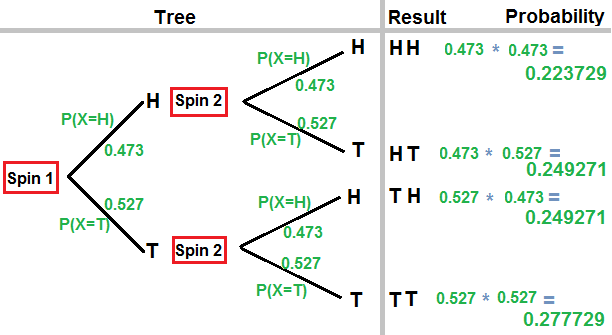
It is also important to realize that the sum of all of the probabilities for the items in the sample space must be 1. This concept is used over and over in our work in statistics. It means, among other things, that if we know that the probability of an event is 0.38 then the probability of getting a result that is not in the event is 1-0.38, that is, 0.62. |

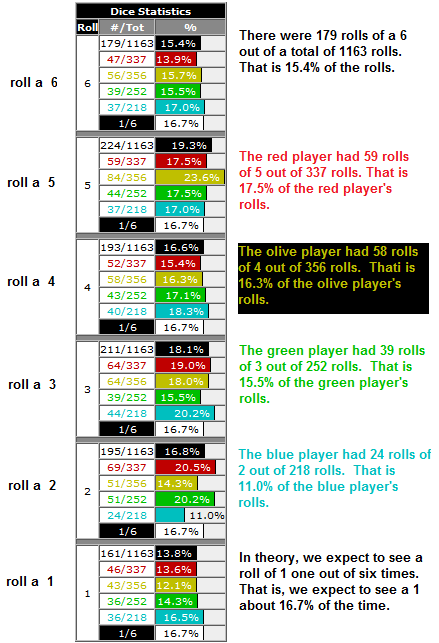
| It is important to note that statistical independence has no meaning beyond that given above. To say that event A is independent of B is just a statement that the probability of event A does not change if we know the value of B. Statistical independence says absolutely nothing about the concept of "cause and effect". This is true even though we fall into the sloppy use of the term dependent when we say that events that are not independent are called dependent. If A is not independent of B then we say A is dependent upon B. This does not mean that B causes or determines A. It just means that if we know the value of B then we may need to adjust our probabilities for the values that A is might have. |