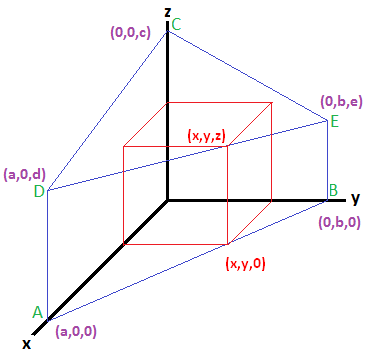
This page walks through solving the cutoff section version of the classic truncated triangular room problem, stated in general terms. The problem is to find the dimensions and size of the largest rectangular box that can be constructed in a truncated triangular room of given dimensions, but where that room has a third "wall" along the hypotenuse of the floor of the room. Such a triangular room still has a right triangle for its floor. Its three walls are trapezoids. The roof is still a triangle. An image of such a room, placed at the origin of a rectangular coordinate system is:

We will solve this problem using the method of Legrange multipliers.

We start with the volume of the box:

`V(x,y,z) = x**y**z`

(1)

Then we have to find the equations of the two planes that make up the roof and the third wall. To find the equation of the plane of the roof we can construct the vectors from point D to C, and from D to E.

At this point we have the three functions V, g, and h, where we are looking to maximize V subject to the constraints of g and h. The Legrange method looks at having `lambda` and `mu` where

`gradV(x_0,y_0,z_0) = lambda * gradg(x_0,y_0,z_0) + mu*gradh(x_0,y_0,z_0)`

(4)

at the solution point `(x_0,y_0,z_0)`. We will form each of these gradients.

Then, based upon (4) we will have to have each of the following three equations be true:

`yz = lambda(bc-bd) + mu(bd)`	(5)
`xz = lambda(ac-ae) + mu(ad)`	(6)
`xy = lambda(ab)`	(7)

and we combine these with the equations for the planes involved:

`( bc-bd ) x + ( ac-ae ) y + ( ab )z = abc`	(8)
`bd x + ad y = adb `	(9)

The five equations, (5) - (9) form a system that we can now solve.

Multiply (5) by `a` and multiply (7) by `(c-d)` to get

Substituting this value of `x` in (14) gives:

Substituting (15) into (13) gives:

Thus we have equations (15), (16), and (17) that allow us to determine the values of `x`, `y`, and `z` from the values of a, b, c, d, and e in the original problem. In a real problem it would be easier to find the value of `x` from (15) and then use that value along with (13) and (14) to find the values of `y` and `z`. Once we have all three values, the value of the volume is just `x*y*z`.

As a small example, consider the room formed by A=(7,0,0), B=(0,4,0), C=(0,0,8), D=(7,0,3), and E=(0,4,5). Using the nomenclature from the diagram at the start of this page, this give a=7, b=4, c=8, d=3, and e=5. From this and using (15) we get `x=(49+-7sqrt(19))/6` or `x~~13.25204877` or `x~~3.081284566`. Of these, clearly the first is not feasible so the second is the only answer. Then using (13) and (14), we get `y~~2.23926312` and `z~~4.11963156` so the volume is approximately `28.42474401`.

Looking at the following table of volumes, based upon values for `x` and `y`, and recognizing that these are values at specific points in the domain, and that values are rounded to 5 decimal places, we have even more confidence in our results:

Unfortunately, there is a major problem with our solution. This is illustrated by another specific example, namely, A=(19,0,0), B=(0,18,0), C=(0,0,20), D=(19,0,1), and E=(0,18,2). Using the nomenclature from the diagram at the start of this page, this give a=19, b=18, c=20, d=1, and e=2. From this and using (15) we get `x=(57+-3sqrt(3))/3` or `x~~29.96965511` or `x~~8.030344885`. Of these, clearly the first is not feasible so the second is the only answer. Then using (13) and (14), we get `y~~10.39230485` and `z~~1.577350269` so the volume is approximately `131.6358614`. However, looking at the following table of volumes, based on values for `x` and `y` we can see a major problem.

All of which goes to show that one cannot just apply rules and formuli.