The Classic Truncated Triangular Room Problem

Return to the Main Math 293 page Revised July 5, 2012
Some images on this page have been generated via AsciiMathML.js.
For more information see: www.chapman.edu/~jipsen/asciimath.html.

This page walks through solving the classic truncated triangular room problem, stated in general terms. The problem is to find the dimensions and size of the largest rectangular box that can be constructed in a truncated triangular room of given dimensions. Such a triangular room has right triangles for its floor and two walls. An image of such a room, placed at the origin of a rectangular coordinate system is:

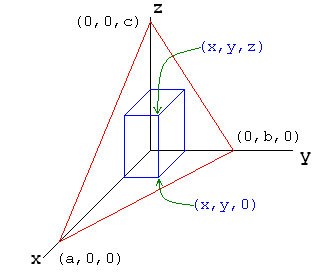
We will solve this problem twice. First, we will solve it by the brute strength and awkwardness techniques of expressing the volume as a function of `x` and `y`, and then finding ordered pairs `(x,y)` that produce zero values for the two partial derivatives of the function. From there we can determine the `z` value and the volume. After that, we will solve it again using the method of Legrange multipliers.

Brute Strength and Awkwardness We start with the volume of the box: `V(x,y,z) = x**y**z` Then we have the equation for the plane: `bc x + ac y + ab z = abc` which we can change to `z = (abc-bc x - ac y) / (ab)` Then we can substitute that expression for `z` into the function for the volume to get `V(x,y,z) = F(x,y) = x**y**((abc-bc x - ac y) / (ab))`
or
`F(x,y) = (abc xy - bc x^2y - ac xy^2) / (ab)`
or
`F(x,y) = c xy - (c/a)x^2y -(c/b)xy^2` So, now we have a function of two variables and we are looking to maximize that function. To do this we want to find all of the points where the partial of F with respect to x and the partial of F with respect to y are 0. But the expression of each of these is: `F_x(x,y) = c y -(2c/a)xy -(c/b)y^2`
`F_y(x,y) = c x -(c/a)x^2 -(2c/b)xy` Setting `F_x(x,y) = 0 ` and factoring we get `0 = c y ** (1 - (2/a x + 1/b y) )` However, whe know `c ne 0` and, since we are looking to find a maximum value, we conclude that `y ne 0`, so we are really only interested in values of `x` and `y` that make `0 = 1 -(2/a)x - (1/b)y` true. Multiplying both sides by `ab` this becomes

`0 = ab - 2b x - ay `

(1)

Setting `F_y(x,y) = 0 ` and factoring we get `0 = c x ** (1 - (1/a x + 2/b y) )` However, whe know `c ne 0` and, since we are looking to find a maximum value, we conclude that `x ne 0`, so we are really only interested in values of `x` and `y` that make `0 = 1 -(1/a)x - (2/b)y` true. Multiplying both sides by `ab` this becomes

`0 = ab - b x - 2ay `

(2)

Then we muliply equation (1) by `2` to get equation (3)

`0 = 2ab - 4b x - 2ay `

(3)

and we subtract (2) from (3) to get `0 = ab - 3bx`
`0 = (a - 3 x) ** b` But we know `b ne 0` so this becomes `0 = a - 3x`
or
`x = (1/3)a` This is an interesting solution in that it means that no matter the dimensions of the original room, the optimal solution will have a box with a length along the x-axis equal to `1/3` the length of that wall (along the floor). Now we can go back to find the required length of `y`. To do this we can substitute our value for `x` into equation (1). `0 = ab - 2b(1/3 a) - a y`
`0 = ab - (2/3) ab - ay`
`0 = (1/3)ab - ay`
`0 = a( 1/3 b - y)` Again, we know `a ne 0` so this becomes `y = (1/3)b` Giving us the depth of the box along the y-axis as `1/3` the length of the that wall. To find the value of `z` we can return to the modified version of the equation of the plane `z = (abc-bc x - ac y) / (ab)` and substitue or values for `x` and `y` to get `z = (abc-bc (1/3)a - ac (1/3)b) / (ab)` Which becomes `z = (abc-(1/3)abd - (1/3)abc) / (ab)` or `z = (1/3)c` Thus the volume is given by `v = (1/3 a)(1/3 b)(1/3 c)`
or
`V = (abc)/27`

Using Legrange Multipliers The second approach to this problem is to solve it using Legrange multipliers. We start with `V(x,y,z) = x*y*z` and we create a new statement of the equation of the plane (this time as a level surface) `g(x,y,z) = bc x + ac y + ab z - abc` which represents the constraint on the original function. These functions then give rise to `grad V(x,y,z) = yz vec i + xz vec j + xy vec k` and `grad g(x,y,z) = bc vec i + ac vec j + ab vec k` The Legrange method is based on having a `lambda` such that `grad V = lambda grad g`. This, in turn, means that we have the following three equations;

`yz = lambda bc`	(4)
`xz = lambda ac`	(5)
`xy = lambda ab`	(6)
along with the equation of the plane (i.e., the constraint)
`bc x + ac y + ab z = abc`	(7)
We solve (4), (5), and (6), respecively, for `lambda` giving rise to:
`(yz)/(bc) = lambda`	(8)
`(xz)/(ac) = lambda`	(9)
`(xy)/(ab) = lambda`	(10)
Using (8) and (9) we have
`(yz)/(bc) = (xz)/(ac)` `y/b = x/a` `a/b y = x`	(11)
Using (9) and (10) we have
`(xz)/(ac) = (xy)/(ab)` `z/c = y/b` `z = c/b y`	(12)
Then, rewiting (7), but substituting `a/b y` for `x` and `c/b y` for `z`
`bc(a/b y) + ac y + ab(c/b y) = abc` `acy +acy +acy =abc` ` 3acy = abc` `y = 1/3 b`	(13)
Subsituting (13) into (11) gives
`x = a/b (1/3 b)` `x = 1/3 a`
Subsituting (13) into (12) gives
`z = c/b (1/3 b)` `z = 1/3 c`
And, of course, all of that gives
max volume is at `(a/3, b/3, c/3)` and that volume is `(abc)/27`