Simple 3 equation 3 variable, with missing varaibles
The main page for solving systems of linear equations on the TI-85 and TI-86.
The previous example page covers a Simple 7 equation 7 variable situation.
The next example page covers a Simple 4 equation 4 variable situation,
but with both missing terms and other variables.
WARNING: The TI-85 and TI-86 are almost identical in their use of the SIMULT function.
The major difference is the labels that are on certain keys. On the TI-85,
SIMULT is the 2nd function on the  key, whereas on the TI-86
SIMULT is the 2nd function on the
key, whereas on the TI-86
SIMULT is the 2nd function on the  key. When a difference is
important it will be presented in the text below. The exception to this is the "3" key. On the
TI-85 it appears as
key. When a difference is
important it will be presented in the text below. The exception to this is the "3" key. On the
TI-85 it appears as 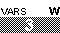 , while on the TI-86 it is
, while on the TI-86 it is
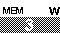 . To save some space, and to ignore this difference, the numeric keys
(the gray ones) have been changed here to only show the key
face, as in
. To save some space, and to ignore this difference, the numeric keys
(the gray ones) have been changed here to only show the key
face, as in  .
In addition, the
.
In addition, the  key will be shown as
key will be shown as  , again to save space.
, again to save space.
Again, this page presents a slight change in the typical
problem of solving a system of linear equations. In this case,
some of the equations are "missing" some of the variables.
The problem we will use on this page is
4x + 7y = 48
3x - 8y + 4z = -50
-5y + 11z = 15
Our first step is to identify the variables. In this case, the
variables are x, y, and z,
although the first equation does not have a z
and the third equation is missing an x term.
Second we need to decide on the order of the varaibles, and the traditional x,
then y, then z
seems reasonable. Third, we can rewrite the equations, with the variables in order, and
not leaving any out. We will add a z term to the first, but with a coefficient of 0.
We will add an x term to the third equation, again with a coefficent of 0. The
rewrite of the problem produces
4x + 7y + 0z= 48
3x - 8y + 4z = -50
0x - 5y + 11z = 15
By adding the extra terms (having 0 as the coefficient) we have not changed any equation
but we have changed the form of the equation so that it fits the same pattern that we
have been using in the earlier pages. We are ready to use the calculator.
Figure 1
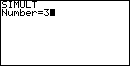
|
The keystrokes to start this process are the same on the two calculators, although
the keys have a different name. For the TI-85 we start with  and
and  , but for the TI-86
we start with , but for the TI-86
we start with  and
and  . On either calculator this selects the "SIMULT" function.
The calculator responds with a request for the
value of "Number" as shown in Figure 1. The SIMULT function expects to have exactly the
same number of equations as we have variables. For our problem, we have 3 variables
and 4 equations. Therefore we respond with the . On either calculator this selects the "SIMULT" function.
The calculator responds with a request for the
value of "Number" as shown in Figure 1. The SIMULT function expects to have exactly the
same number of equations as we have variables. For our problem, we have 3 variables
and 4 equations. Therefore we respond with the  key to complete
Figure 1. key to complete
Figure 1.
|
Figure 2

| We leave Figure 1 by pressing the  key.
That will cause the display to change to Figure 2. Notice in Figure 2 that the
calculator is requesting values for each of the coefficients and constants
that we have in the general standard form for our first equation. The first
subscript on each of the "a's" and the subscript on the "b" indicates that we
are looking at values for the first equation. key.
That will cause the display to change to Figure 2. Notice in Figure 2 that the
calculator is requesting values for each of the coefficients and constants
that we have in the general standard form for our first equation. The first
subscript on each of the "a's" and the subscript on the "b" indicates that we
are looking at values for the first equation.
Remember that we need to put the values in according to the standard form.
Therefore we want the values 4, 7, 0, and 48. The key sequence
 
 
 

 accomplishes this and leaves the display
as in Figure 2. accomplishes this and leaves the display
as in Figure 2.
|
Figure 3

| We move from Figure 2 to Figure 3 by first pressing the  key. Here we need to enter the coefficients and constants for the second
equation, in our standard form, namely 3, -8, 4, and -50. We use the
keys
key. Here we need to enter the coefficients and constants for the second
equation, in our standard form, namely 3, -8, 4, and -50. We use the
keys
 
  
 
 
 to complete the image of Figure 3. to complete the image of Figure 3.
Now we can move to the next screen by
pressing the  key. key. |
Figure 4

| Here we need to enter the coefficients and constants for the third
equation, in our standard form, namely 0, -5, 11, and 15. We use the
keys
 
  
  
  to complete the image of Figure 4. And, at this point we are ready to solve the
system of linear equations.
to complete the image of Figure 4. And, at this point we are ready to solve the
system of linear equations. |
Figure 5

| We request a solution by pressing the  key.
The calculator determines the correct answer and displays it as Figure 5. key.
The calculator determines the correct answer and displays it as Figure 5.
Once again we need to return to our standard form and recognize that
x1 is x,
x2 is y, and
x3 is z. Therefore,
we have a unique solution to all three equations when
x=-2,
y=8, and
z=5. |
The main page for solving systems of linear equations on the TI-85 and TI-86.
The previous example page covers a Simple 7 equation 7 variable situation.
The next example page covers a Simple 4 equation 4 variable situation,
but with both missing terms and other variables.
©Roger M. Palay
Saline, MI 48176
October, 1998
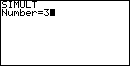
 and
and  , but for the TI-86
we start with
, but for the TI-86
we start with  and
and  . On either calculator this selects the "SIMULT" function.
The calculator responds with a request for the
value of "Number" as shown in Figure 1. The SIMULT function expects to have exactly the
same number of equations as we have variables. For our problem, we have 3 variables
and 4 equations. Therefore we respond with the
. On either calculator this selects the "SIMULT" function.
The calculator responds with a request for the
value of "Number" as shown in Figure 1. The SIMULT function expects to have exactly the
same number of equations as we have variables. For our problem, we have 3 variables
and 4 equations. Therefore we respond with the  key to complete
Figure 1.
key to complete
Figure 1.

 key.
That will cause the display to change to Figure 2. Notice in Figure 2 that the
calculator is requesting values for each of the coefficients and constants
that we have in the general standard form for our first equation. The first
subscript on each of the "a's" and the subscript on the "b" indicates that we
are looking at values for the first equation.
key.
That will cause the display to change to Figure 2. Notice in Figure 2 that the
calculator is requesting values for each of the coefficients and constants
that we have in the general standard form for our first equation. The first
subscript on each of the "a's" and the subscript on the "b" indicates that we
are looking at values for the first equation.






 accomplishes this and leaves the display
as in Figure 2.
accomplishes this and leaves the display
as in Figure 2.

 key. Here we need to enter the coefficients and constants for the second
equation, in our standard form, namely 3, -8, 4, and -50. We use the
keys
key. Here we need to enter the coefficients and constants for the second
equation, in our standard form, namely 3, -8, 4, and -50. We use the
keys









 to complete the image of Figure 3.
to complete the image of Figure 3.
 key.
key. 









 to complete the image of Figure 4. And, at this point we are ready to solve the
system of linear equations.
to complete the image of Figure 4. And, at this point we are ready to solve the
system of linear equations. 
 key.
The calculator determines the correct answer and displays it as Figure 5.
key.
The calculator determines the correct answer and displays it as Figure 5. 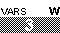 , while on the TI-86 it is
, while on the TI-86 it is
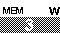 . To save some space, and to ignore this difference, the numeric keys
(the gray ones) have been changed here to only show the key
face, as in
. To save some space, and to ignore this difference, the numeric keys
(the gray ones) have been changed here to only show the key
face, as in  key will be shown as
key will be shown as