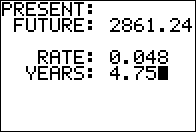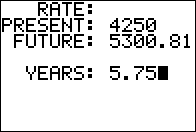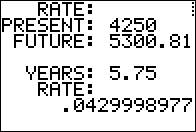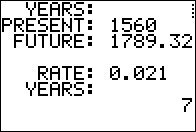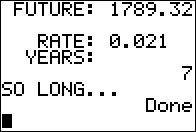Figure 01
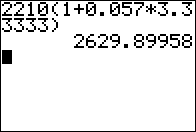
|
Invest, at simple interest, $2210 at 5.7% for 3 years and 4 months.
Find the future value of that investment?
Use the formula
FV = PV(1 + R*T).
On the caluclator we evaluate
2210(1+0.057*3.33333),
as shown in Figure 01,
which gives FV the value $2629.90, rounded to the nearest cent if need be.
|
Figure 02
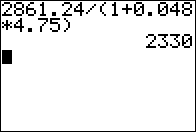
|
What present value is required to end up with $2861.24
if we invest at simple interest at 4.8% for 4 years and 9 months?
Use the equation PV = FV/(1 + R*T).
On the calculator evaluate the expression
2861.24/(1+0.048*4.75), as shown in Figure 02,
which gives PV the value $2330.
|
Figure 03
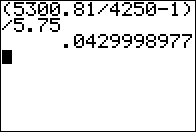
|
What rate is required to end up with $5300.81
if we invest $4250 for 5 years and 9 months?
Use the equation R = (FV/PV - 1)/T .
On the calculator, in Figure 03, evaluate the expression
(5300.81/4250-1)/5.75 which gives R the value 0.043 or 4.3%.
|
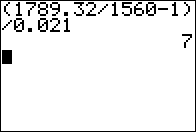
Figure 04
|
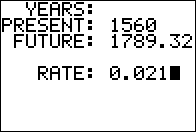
What time is required to end up with $1789.32 if we invest
$1560 at 2.1%?
Use the formula
T = (FV/PV - 1)/R .
On the calculator evaluate
(1789.32/1560-1)/0.021, which gives T the value 7.00000 or 7 years.
|
Figure 05
|
To run the program, once it is loaded onto your calculator, find and highlight
the name in the PRGM menu. Then press
 to paste the command onto the main screen,
shown in Figure 06. to paste the command onto the main screen,
shown in Figure 06.
|
Figure 06

|
Now that the command is in place press  to have the calculator start to rn the program.
to have the calculator start to rn the program.
|
Figure 07

|
In Figure 07 we see the menu that was specified in line 7 of the program.
We can select an item of the menu by typing its number or by highlighting
the desired item and pressing the  key.
We will start with the first option, FUTUTRE VALUE to do the first problem
(from back in Figure 01) where we need to find the future value. key.
We will start with the first option, FUTUTRE VALUE to do the first problem
(from back in Figure 01) where we need to find the future value.
|
Figure 08

|
The program clears the screen and starts to ask for the
required values, the first of which is the present value.
|
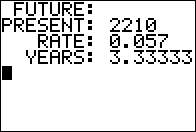
Figure 09
|
Figure 09 shows the status of the screen after we have given
the program after all the needed values. Press
 to continue. to continue.
|
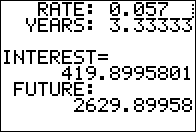
Figure 10
|
Figure 10 shows the intermediate value,
namely the interest, and the desired answer, the future value
After reading the answer we press
 and the program takes us back to
the menu, shown again in Figure 11. and the program takes us back to
the menu, shown again in Figure 11.
|
Figure 11

|
The next problem will be the one to find the present value,
the second option on the menu.
|
Figure 12
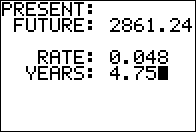
|
Figure 12 shows that we entered the same information
that we had in Figure 02.
|
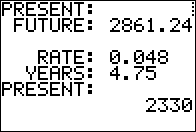
Figure 13
|
We see the answer in Figure 13.
From there we would press  , return to the menu screen,
and then select the third option to solve the
problem given in Figure 03. , return to the menu screen,
and then select the third option to solve the
problem given in Figure 03.
|
Figure 14
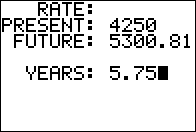
|
Figure 14 shows the data from the problem.
|
Figure 15
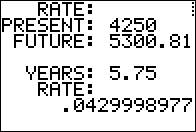
|
Figure 15 shows the answer.
Again, pressing  retyurns us to the menu where we choose the fourth
option to move to Figure 16.
retyurns us to the menu where we choose the fourth
option to move to Figure 16.
|
Figure 16
|
We enter the required data.
|
Figure 17
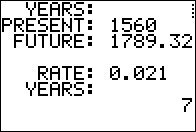
|
Figure 17 shows the answer.
|
Figure 18
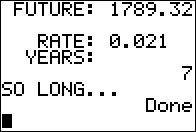
|
And, just for completeness, Figure 18 shows the result of choosing option
5: QUIT from the menu.
|
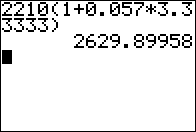
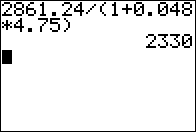
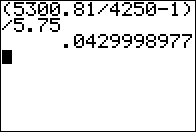


 to paste the command onto the main screen,
shown in Figure 06.
to paste the command onto the main screen,
shown in Figure 06.