Financial: Effective Rate

Return to Roadmap 5

Consider investing in one of the following four banks:

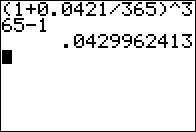
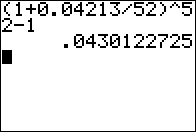
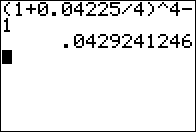
BANK A

Invest with us!
We pay 4.21%
compounded daily

BANK B

Invest with us!
We pay 4.213%
compounded weekly

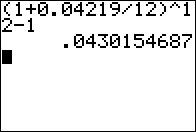
BANK C

Invest with us!
We pay 4.219%
compounded monthly

BANK D

Invest with us!
We pay 4.225%
compounded quarterly

Back in the days when you did not have a fancy calculator or access to various web pages the decision about which bank to choose was quite confusing. To help consumers make a reasonable decision, the government insisted that any such add, or any contract involving compound interest, must include an effective rate, also known by the more popular name, the annual percentage rate or the APR. The effective rate, that is, the APR, is the simple interest rate that would produce the same results over one yeat that the advertised compound interest rate would produce over that same year. Including the effective rate changes the adds to

BANK A

Invest with us!
We pay 4.21%
compounded daily
4.29962% APR

BANK B

Invest with us!
We pay 4.213%
compounded weekly
4.301227% APR

BANK C

Invest with us!
We pay 4.219%
compounded monthly
4.301547% APR

BANK D

Invest with us!
We pay 4.225%
compounded quarterly
4.29241% APR

(Sorry I couldn't resist putting the APR in small letters as is so commonly done in the real world.) Now it is easy to compare the offers: Bank C is clearly offering the highest rate. So now, our only question is "How do we compute the effective rate, the APR. The answer to that is to apply the algorithm for computing the compound interest to an investment of $1 for one year. Then, look at the amount of interest earned in that year. That will be the effective rate. The algorithm for finding the the future value is given by FV_n = PV₁(1 + r/t)ⁿ But for an investment of $1 for 1 year the right side of this becomes (1 + r/t)^t Then, taking away the original $1 investment gives us the amount of interest earned in that year as (1 + r/t)^t – 1 This means that we could calculate the effective rate for the four banks as shown in Figures 01 through 04.

Figure 01	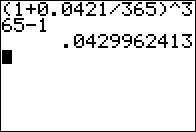Computation for Bank A.
Figure 02	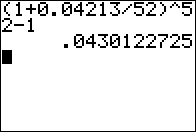Computation for Bank B.
Figure 03	Computation for Bank C.
Figure 04	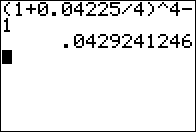Computation for Bank D.

As we have seen in earlier examples, it is probably better to capture this algorithm in a program than it is to try to remember the formula and to type it in for each new problem. Rather than write a whole new program we could just modify the COMPOUND program. To do this we would change the menu line to contain

and we would insert the following lines toward the end of the program

Then, we could run the program and choose the EFFECTIVE option to get Figureq 05 through 08.

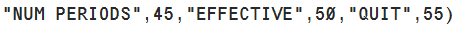
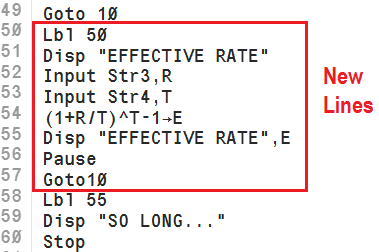
Figure 05	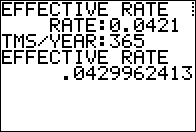Using the mdified program for the values for Bank A.
Figure 06	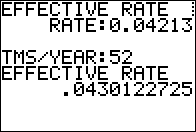Using the mdified program for the values for Bank B.
Figure 07	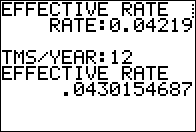Using the mdified program for the values for Bank C.
Figure 08	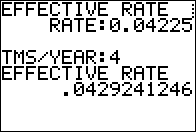Using the mdified program for the values for Bank D.