Battleship Game Fixed Solution

The Battleship Game was explained on an earlier page, namely at battleexplain. That explanation included an approach to finding the battleship based upon two guesses, one at the lower left corner of the ocean and the other at the lower right corner of the ocean. That particular approach could be termed "investigative" since we determine the required sum of perfect integer squares and then examine the list of such perfect integer squares to see if we can find pairs of such values that yield the desired sum. This page presents a solution for the same situation, but a solution that is computational instead of investigative.

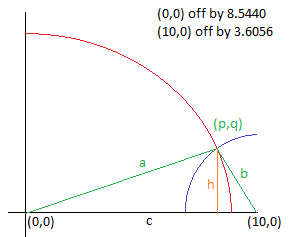
This approach uses the area of the triangle formed by the location of the battleship and the two lower corner point guesses. Thus, for a ship in the first quadrant, we might have the following situation:

Thus, we have two guesses, one at (0,0) which is off by 8.5440 and the second at (10,0) which is off by 3.6056. The drawing shows the possible points from the first guess as the red arc and the possible points for the second guess as the blue arc. The location of the battleship is given as (p,q). Thus, we have a triangle with corners at (0,0), (10,0), and (p,q). The diagram also contains the "altitude" of the triangle, marked as "h". We might note that the value of "q" is exactly "h". In addition, we have marked the sides as a, b, and c. The length of a is 8.5440, the length of b is 3.6056, and the length of c is 10.

Recall that the area of the triagle is one half the base times the height. In our case, that means that the area of the triangle is

(1/2)*c*h, or
(1/2)(10)(h). There is another formula for the area of a triangle. This is Heron's formula, one form of which uses the semi-perimeter of the triangle along with the length of each of the sides of the triangle. The semi-perimeter is just half the perimeter, or in our case s=(1/2)(a+b+c) then, Heron's formula is area of triangle= sqrt(s*(s-a)*(s-b)*(s-c)) In the case given above, the value of the semi-perimeter is s=(8.5440+3.6056+10)/2, or
s=22.1495/2, or
s=11.07475 Then the area of the triangle is sqrt(11.07475*(11.07475-8.5440)*(11.07475-3.6056)*(11.07475-10)), or
sqrt( 11.07475*2.53075*7.46925*1.07475 ), or
sqrt(224.992285), or
14.99974 We know that is an approximate answer and we know that since h is an integer and 10/2 is 5 then that the area must also be an integer. Therefore, by Huron's formula, the area of the triangle is 15 square units. Returning to the usual formul for the area of a triangle, namely, area = (1/2)(base)(height) for our triangle we have 15= (1/2)(10)h, or
15=5h, or,
3=h. Because h=q we now know that the location of the battleship is at the point (p,3). Furthermore, we know that a² = p² + q², or
8.544² = p² +3², or
72.999936 = p² + 9, or, correcting for the approximate values
73 = p² + 9, or
64 = p², or
8 = p. . Therefore, the battleship is at the point (8,3).

The beauty of this approach is that it is entirely computational. There is no "searching for possible solutions. As long as we are given the distance from the lower left corner to the ship and from the lower right corner to the ship we can just compute the location of the ship. This means that we can construct a program for our calculator that will take the initial information and produce the location of the ship. Below is an annotated program to do exactly this. Note that the program merely walks through the same steps that we took above.

This particular program is stored in the file batfsol.8xp. Here is a record of running that program, first for the problem given above and then for a problem on the larger ocean.

Figure 1	Figure 1 shows the start of the program. It is now waiting for us to enter the coordinates of the lower left corner.
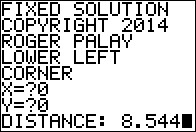Figure 2	In Figure 2 we have entered the coordinates of the lower left corner and the distance from that corner to the ship.
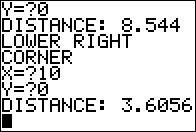Figure 3	In Figure 3 we have entered the coordinates of the lower right corner and the distance from that cornerr to the ship.
Figure 4	The program displays the location of the ship, at point (8,3). It then continues to try a new problem. For the new problem we will consider the "ocean" to be from (-10,-10) to (10,-10) to (10,10) to (-10,10). Our first guess is the lower left corner, point (-10,-10). The "battleship" game tells us that we are off by 17.0294 units. The we guess the lower right corner, point (10,-10). The game tells us we are off by 3.1623 units. Where is the ship?
Figure 5	For Figure 5 we have given our program the coordinates of the lower left corner, (-10,-10) and the distance, 17.0294, from that point to the ship.
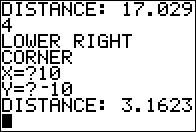Figure 6	For Figure 6 we have given the program the coordinates of the lower right corner, (10,-10), and the distance from that point to the ship, namely, 3.1623.
Figure 7	The program responds with the location of the ship at (7,-9).