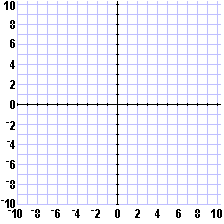


| In Figure 1 we have started the program. The calculator has placed the ship and it has asked for our guess. |

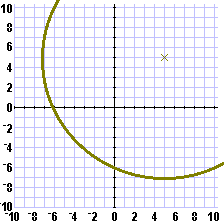
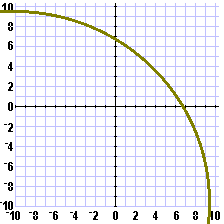
| In Figure 2 we have made our guess at the point (5,5),
and the calculator has informed us that the distance
from our guess to the ship is approximately 12.1655 units.
That means that the ship is located somewhere on a
circle with center at (5,5) and with a radius of 12.1655 units.
We have graphed part of such a circle below.
 |

| Figure 3 shows that next guess and the calculator response that
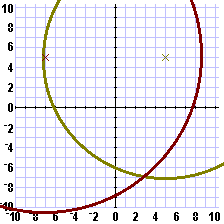 |

| In Figure 4 the player has used an unnecessary
guess, at (7,– 7). This guess is
off from the battleship by exactly 4 units. The graph above has been
modified to add the circle with center at (7,– 7)
and radius equal to 4 to give:
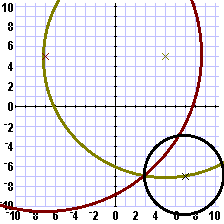 |

| Figure 5 confirms our computed answer. |
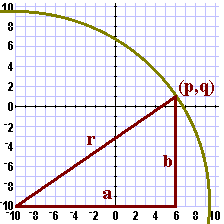
As in the earlier web page describing the BAT1F program,
we would like to be able to compute an answer without having to draw the graphs.
In that earlier page we noted that if we make a guess at the lower left of the
playing field, that is,
at
| number | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| number2 | 0 | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 | 121 | 144 | 169 | 196 | 225 | 256 | 289 | 324 | 361 | 400 |

| Figure 6 shows the start of a new game. The first guess
is at the lower left corner of the playing field,
|
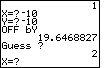
| Our guess turns out to be 19.64688 units away from the ship.
That is the value of r is approximately, 19.64688 units.
We can computer 19.646882 and we find that it is approximately 385.999.
We know that r2 is an integer.
Thus, we recognize that r2=386.
We need to find two perfect squares of integers that add to give 386. We can look at the second row of the table above
and find that 386=25+361. That is,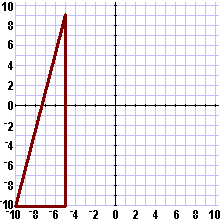 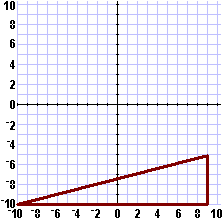 |

| The next guess is at |

| Here is a confirmtion of our calculation. |
| As usual, to get out of the program, press the
 key. This will bring up the screen shown in Figure 10.
Press the key. This will bring up the screen shown in Figure 10.
Press the  key to quit and return to
normal calculator operation. key to quit and return to
normal calculator operation. |
©Roger M. Palay
Saline, MI 48176
May, 2001