Battleship: BAT1F on the TI-83

Figure 1	In Figure 1 we have started the program. The calculator has placed the ship and it has asked for our guess. In this case we have guessed the point (5,5). Once we press the key to accept the y-coordinate, we will move to Figure 2.
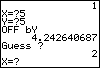
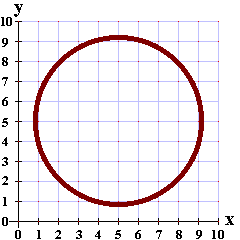
Figure 2	The calculator reports that we have missed the battleship by about 4.2426 units. That means that the ship is on a circle with center at (5,5) and radius 4.2426. We have graphed such a circle below.
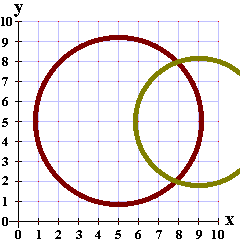
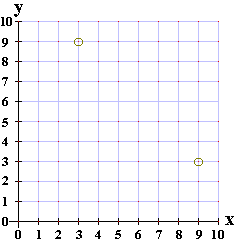
Figure 3	In Figure 3 we have chosen our second guess as the point (9,5). This time we are off by about 3.162 units. Therefore, we have drawn part of a second circle below, this one with center at (9,5) and with a radius 3.162. The two circles cross at (8,8) and (8,2). The battleship must be at one of these points.
Figure 4	Our next guess, as shown in Figure 3, is (8,2) and we were lucky enough to get hit. The calculator is ready for a new game.
Figure 5	Again, we guess the point (5,5). This time we are off by approximately 4.4721 units.
Figure 6	We have drawn a circle with center at our guess, (5,5) and with radius 4.4721. From this we can see that there are a number of possible locations for the battleship. We can also see that the point (9,5) is not a possible solution. However, if we guess (9,5) we will get the distance from (9,5) to the battleship.
Figure 7	In Figure 7 we have made the guess at (9,5) and we find that the distance from (9,5) to the battleship is about 7.2111. Therefore we can draw part of the circle with center at (9,5) and having a radius of about 7.2111. The new graph is given as: It should be clear from this picture that the battleship is either at the point (3,9) or it is at the point (3,1).
Figure 8	Unfortunately, the person playing this game decided to try the point (2,5). Fromn Figure 8 we note that (2,5) misses the ship by 4.123 units. Therefore, we can graph part of the circle with center at (2,5) and radius equal to 4.123. This confirms the two possible locations for the ship.
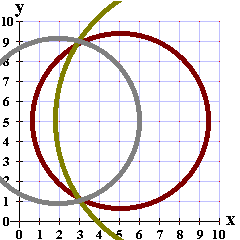Figure 9	Still not believing the graph, the player has guessed (3,5) only to discove that they have missed the ship by 4 units.
Figure 10	Finally, we arrive at a guess of (3,9). Luckily the ship has been hit. Please note that with the information that we had, it was just as likely that the ship was at (3,1).
Figure 11	Our player seems to have been tired of the game. To get out of the game we press the key. This will bring up the screen shown in Figure 11. We want the first option, Quit. Therefore, press to select that highlighted option.

The process shown above works quite well. It has the disadvantage of finding many possible solutions. We can develop a different approach that will cut down the number of possible solutions. We will do this by making our guesses at the two lower corners of the playing field, namely at (0,0) and at (10,0).

Figure 12	In Figure 12 we have started the game again.
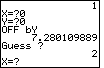
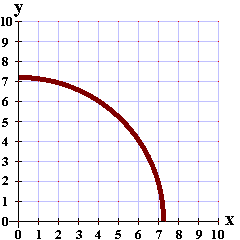
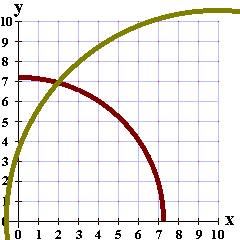
Figure 13	Having guessed (0,0) and finding out that we missed the battleship by 7.28 units, we can draw an arc on the graph with center at (0,0) and radius equal to 7.28 units. Notice that we have just 1/4 of a circle here.
Figure 14	The next guess, (10,0), misses the ship by 10.63 units. Again we can draw an arc covering all possible locations for the ship. In this case the two arcs intersect at exactly one point; the ship must be at the point (2,7).
Figure 15	Our observation is confirmed in Figure 15.

Figures 13 through 15 demonstrate the advantage of guessing at the lower left and lower right corners of the playing area. However, we are left with the need to draw the two arcs in order to make our final guess. We would like to find some way to determine the location of the ship without having to use a drawing.

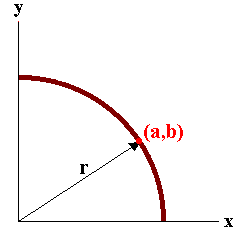
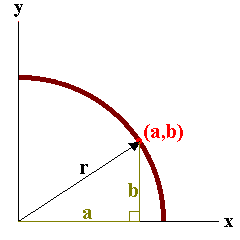
The image below represents a guess at the point (0,0) with the result of missing the ship by r units.

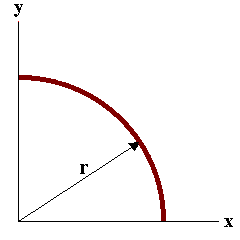
Figure 16	We start the game and make our initial guess at (0,0).
Figure 17	We are off by approximately 9.4868 units. This is the value of r. We can compute (on another calculator) the value of r2 and we find that 9.48682 = 89.99937424 and because we know that r2 must be an integer, we can convert that approximation to r2 = 90 We recall that a2 + b2 = r2 and that the point (a,b) must have integer coordinates. Therefore, we need to find values for a and b so that a2 + b2 = 90 We can look at the following table: number 0 1 2 3 4 5 6 7 8 9 10 number2 0 1 4 9 16 25 36 49 64 81 100 and we can see that the only way to have two numbers in the bottom row add to 90 is to use 81 and 9. Therefore, either a=9 and b=3 or a=3 and b=9. This means that the ship is either at the point (3,9) or it is at the point (9,3).
Figure 18	In Figure 10 we have the second guess, this one at (10,0). This guess is off by about 3.162 units. Remember that our two possible points are (3,9) and (9,3). The first point is too far away from the guess at (10,0). The second point, (9,3), could certainly be about 3.162 units from (10,0). We can construct a right triangle as shown below. We use a calculator to determine that 3.1622 is 9.998244. Knowing that the original distance given by the calculator was merely an approximation, we recognize that 9.998244 is an approximation to 10. Therefore, the numbers that we have found conform to the Pythagorean Theorem, namely, (3)2 + (1)2 = (3.162...)2 9 + 1 = 10 This should confirm that the only possible location for the ship is at the point (9,3).
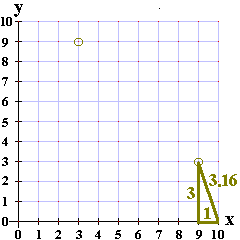Figure 19	In Figure 19 we have guessed the point (9,3) and we have hit the ship at that location.
Figure 20	We start another game in Figure 20. This time, our guess of (0,0) missed the ship by about 5.83095 units. 5.830952 is about 33.9999779. Therefore, we know that we are looking at triangle where the square of the hypotenuse (the side opposite the right angle) is 34. We need to find two perfect squares from the table number 0 1 2 3 4 5 6 7 8 9 10 number2 0 1 4 9 16 25 36 49 64 81 100 that add up to 34. A quick examination shows us that 9+25=34. Therefore, the two sides of the triangle are 3 and 5 units long. Because our guess was (0,0), the ship must be at either the point (3,5) or the point (5,3).
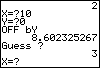
Figure 21	Now we guess the point (10,0), only to find that we have missed the ship by about 8.6023 units. 8.60232 is about 73.99956, which we round off to 74. If we look at the table of squares, we see that 74=25+49. Therefore, the triangle from (10,0) to the location of the ship and then down to the x-axis must have sides of 5 and 7 units. Starting from (10,0) we can come back 5 units and go up 7 to get to the point (5,7). That point is the right distance from (10,0) but it was not one of the points we found before. The other alternative, starting at (10,0), going back 7 units on the x-axis and then moving up 5 units, puts us at the point (3,5), which was one of the possible locations. Therefore, we are certain that the ship is at the point (3,5).
Figure 22	Figure 22 confirms our computations.
Figure 23	Figure 23 starts a final example. Again we start with a guess of (0,0). This time we missed the ship by about 8.0623 units. We find that 8.06232 is about 65.0007, which we round off to 65. We are looking for pairs of values in the table of squares that add to give 65. In this case there are two such answers. We have 65 = 64 + 1 and 65 = 49 + 16 Therefore, the sides of the right triangle will be either 8 and 1 or they will be 4 and 7. This means that we have 4 possible locations for the ship: (1,8), (8,1), (4,7), and (7,4). Each of these points is about 8.0623 units from (0,0).
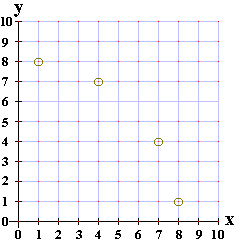Figure 24	Our second guess, at (10,0), is off by about 9.2195. We compute 9.21952 to be about 84.99918, which we round to 85. The perfect squares that add to 85 are 81+4 and 49+36. This means that the triangle from (10,0) to the ship and then down to the x-axis will have sides of length 8 and 2, or sides of length 7 and 6. Using the lengths 8 and 2, and starting from (10,0), we can move back 8 and up 2 to get to the point (2,2), or we can move back 2 and up 8 to get to the point (8,8), but neither point is one of our possible points. on the other hand, if we use lengths 7 and 6, starting at (10,0) we can move back 7 and up 6 to get to the point (3,6) or we can move back 6 and up 7 to get to the point (4,7). Of these, only the point (4,7) was a possible solution from before. Thus, our answer is (4,7).
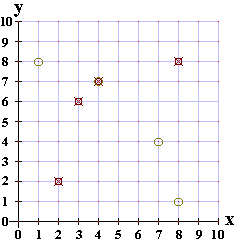Figure 25	Figure 25 confirms our computations.

A slightly more difficult version of this program places the ship into a playing field that contains portions of all four quadrants. The bat2f page describes and demonstrates solutions for this alternate version.