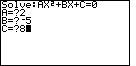Figure 1

|
We start in Figure 1 with the result of using the
key sequence   .
The poly key command walks us through a process of solving a polynomial
equation. The first thing that we need to do is to tell the calculator
the "order" or "degree" of the polynomial. That is, what is the "order"
or "degree" of the highest term in the polynomial? .
The poly key command walks us through a process of solving a polynomial
equation. The first thing that we need to do is to tell the calculator
the "order" or "degree" of the polynomial. That is, what is the "order"
or "degree" of the highest term in the polynomial?
|
Figure 2

| The polynomial equation that we want to solve is
2x2 + 5x – 3 = 0
Therefore, this is a second order polynomial, and our response to the
prompt is  . . We finish this screen and move to Figure
3 via the  key. key.
|
Figure 3
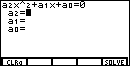
| The calculator responds by showing us a
standard, second order polynomial equation, namely
a2x^2+a1x+a0=0
and then asking for values for the three coefficients,
a2, a1, and a0.
|
Figure 4
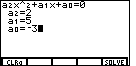
| Our equation is
2x2 + 5x – 3 = 0
which means that
a2 is 2, a1 is 5, and a0 is
– 3. Figure 4 shows those values having been entered at
the appropriate line of the display.
|
Figure 5

| In Figure 4 we gave the calculator the values for the numeric
coefficients. Now we press the  key
to select the fifth menu option, SOLVE. This
produces the screen shown in Figure 5. This output is quite convenient
in that it gives us a row of output for each of the answers to the
equation. key
to select the fifth menu option, SOLVE. This
produces the screen shown in Figure 5. This output is quite convenient
in that it gives us a row of output for each of the answers to the
equation. |
Figure 6

| To create Figure 6 we have merely typed out the entire command.
The keys  
 shift and lock the calculator in
lower case alphabetic mode.
The keys shift and lock the calculator in
lower case alphabetic mode.
The keys  
  produce the word
poly. We leave alphabetic mode by pressing the produce the word
poly. We leave alphabetic mode by pressing the
 key. We open the LIST menu by pressing
the key. We open the LIST menu by pressing
the   keys.
This displays the menu shown in Figure 6. We can use that menu, via
the keys.
This displays the menu shown in Figure 6. We can use that menu, via
the  key to paste aleft brace, {, onto the
screen.
Now we enter the values for the coefficients, separated by commas, as in key to paste aleft brace, {, onto the
screen.
Now we enter the values for the coefficients, separated by commas, as in
 
 amd amd  .
The .
The  selects the closing right brace, },
from the menu. With that we have constructed the poly command. selects the closing right brace, },
from the menu. With that we have constructed the poly command.
|
Figure 7

| Having constructed the command in Figure 6, we need only press the
 key to perform the command, and to display the
results as can be seen in Figure 7. Note that the result is given as a "list"
of values. The numbers are the same as we saw in Figure 5, but there the values
were displayed as separate items, one item to each line of the display. key to perform the command, and to display the
results as can be seen in Figure 7. Note that the result is given as a "list"
of values. The numbers are the same as we saw in Figure 5, but there the values
were displayed as separate items, one item to each line of the display.
|
Figure 8

| One of the advantages of having the "list" of solutions is that we can
obtain the values in fractional format. In Figure 8 we have
used the   keys to recall the previous command, the
keys to recall the previous command, the
 key
to open the CUSTOM menu, the key
to open the CUSTOM menu, the  key to select our
first menu option, key to select our
first menu option, 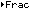 , and
finally, the , and
finally, the  key to perform the command
that we constructed.
The result is shown in Figure 8, where we can see the value of one-half being displayed
as 1/2. key to perform the command
that we constructed.
The result is shown in Figure 8, where we can see the value of one-half being displayed
as 1/2.
|
Assuming that we have lots of poynomials to solve, it might be nice to put the
"poly" command into our CUSTOM menu. Figures 9 through 12 step us through this process.
Figure 9

| In order to put the "poly" command into the CUSTOM menu we first
need to find it in the CATALOG. We do this by openning the CATALOG menu via
the   keys.
The menu is shown in Figure 9. keys.
The menu is shown in Figure 9. |
Figure 10

| We move forward by pressing the  key to open the CATALOG. Within the CATALOG we want to find the "poly"
command. We can move directly to the "P" entries by
pressing the
key to open the CATALOG. Within the CATALOG we want to find the "poly"
command. We can move directly to the "P" entries by
pressing the  key. That will leave us with a
screen as shown in Figure 10. key. That will leave us with a
screen as shown in Figure 10.
|
Figure 11

| Either the cursor down key,  ,
or the ,
or the  key (selecting option 1 from the menu) can
be used to move down the list until we have displayed and selected the "poly"
command, as shown in Figure 11. Then we need to open the
CUSTOM menu, via the key (selecting option 1 from the menu) can
be used to move down the list until we have displayed and selected the "poly"
command, as shown in Figure 11. Then we need to open the
CUSTOM menu, via the  key. key.
We note in Figure 11 that there are open spots in the CUSTOM menu.
We will place the "poly" command into the second
spot by pressing the  key.
The result is shown in Figure 12. key.
The result is shown in Figure 12. |
Figure 12

| Figure 12 shows us that we have placed the "poly" command into the
second slot of the CUSTOM menu. We use the  key
a number of times to get out of the menus displayed at the bottom of the screen. key
a number of times to get out of the menus displayed at the bottom of the screen.
|
Figure 13
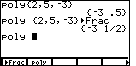
| Having left the CATALOG menu from Figure 12, we can open the CUSTOM
menu in Figure 13 by pressing the  key.
Then it is a simple matter, pressing the key.
Then it is a simple matter, pressing the  key to paste the "poly" command onto the screen.
key to paste the "poly" command onto the screen. |
Figure 14
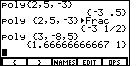
| Figure 14 shows the calculator display after we have
completed entering the values for the equation
3x2 – 8x + 5 = 0
Notice that we have openned the LIST menu so that we now
have the curly braces in our menu, and that we entered the coefficients
as values in a list. Having typed the command, we press the ENTER
key to obtain the answer. The last output line in Figure 14 gives the
decimal approximation to the answer. |
Figure 15
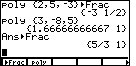
| We can change the answer to fractional form via the
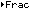 command, which we had stored in
the CUSTOM menu. Figure 15 shows the result of returning to the CUSTOM
menu via the command, which we had stored in
the CUSTOM menu. Figure 15 shows the result of returning to the CUSTOM
menu via the  key, and pressing the key, and pressing the
 key to select the key to select the 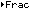 menu option. Pressing the
menu option. Pressing the  key will produce the
complete output in Figure 15. key will produce the
complete output in Figure 15.
|
Figure 16
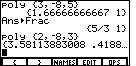
| In Figure 16 we are attempting to find the solutions for
2x2 – 8x + 3 = 0
Notice that the two decimal approximations to the answers do not fit onto the screen.
[Recall that when we used the "poly" key sequence that the solutions were listed, one per line,
down the page, but that the result of the "poly" command is a list that holds the solutions.] |
Figure 17
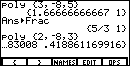
| Naturally, we can use the  key to see the rest of the answer from Figure 16. We have done just that
to obtain the image in Figure 17.
key to see the rest of the answer from Figure 16. We have done just that
to obtain the image in Figure 17. |
Figure 18
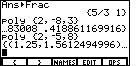
| Now we will look at the solution to the equation
2x2 – 5x + 8 = 0
Figure 18 shows both the "poly" command and the resulting answer.
In this case the answer is a pair of imaginary (complex) numbers.
|
Figure 19
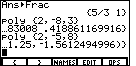
| The display for Figure 19 shows the rest of the answer from Figure 18.
|
Figure 20

| For Figure 20 we have started the the QUAD program. (More information
on the QUAD program for the TI-86 and TI-85 can be
found on the 208606.htm page.)
We have entered the values for the coefficients. We still need to
press the  key to move on to Figure 21. key to move on to Figure 21. |
Figure 21

| The QUAD program calculates the discriminant and, recognizing
that the discriminant is negaitve, that program merely tells us that there is no real
solution. |
Figure 22

| QUAD1 is a more elaborate program.
(More information
on the QUAD1 program can be
found on the 208607.htm page.)
In Figure 22 we have started that program and entered the values into it.
|
Figure 23

| Again the result is that there are no real solutions. |
Figure 24
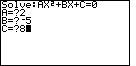
| Figure 24 has the start of the QUAD2 program.
(More information
on the QUAD2 program can be
found on the 208608.htm page.)
Again we have entered the coefficients. |
Figure 25
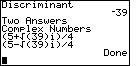
| Unlike the earlier programs, QUAD2 is happy to process quadratic
equations that have complex number solutions.
In Figure 25 we see those two solutions, not as decimal approximations, as in
Figures 18 and 19, but as complex numbers, including the square root of 39.
|


 .
The poly key command walks us through a process of solving a polynomial
equation. The first thing that we need to do is to tell the calculator
the "order" or "degree" of the polynomial. That is, what is the "order"
or "degree" of the highest term in the polynomial?
.
The poly key command walks us through a process of solving a polynomial
equation. The first thing that we need to do is to tell the calculator
the "order" or "degree" of the polynomial. That is, what is the "order"
or "degree" of the highest term in the polynomial?

 .
.  key.
key.



 key
to select the fifth menu option, SOLVE. This
produces the screen shown in Figure 5. This output is quite convenient
in that it gives us a row of output for each of the answers to the
equation.
key
to select the fifth menu option, SOLVE. This
produces the screen shown in Figure 5. This output is quite convenient
in that it gives us a row of output for each of the answers to the
equation. 




 produce the word
poly. We leave alphabetic mode by pressing the
produce the word
poly. We leave alphabetic mode by pressing the
 keys.
This displays the menu shown in Figure 6. We can use that menu, via
the
keys.
This displays the menu shown in Figure 6. We can use that menu, via
the  key to paste aleft brace, {, onto the
screen.
Now we enter the values for the coefficients, separated by commas, as in
key to paste aleft brace, {, onto the
screen.
Now we enter the values for the coefficients, separated by commas, as in
 amd
amd  .
The
.
The  selects the closing right brace, },
from the menu. With that we have constructed the poly command.
selects the closing right brace, },
from the menu. With that we have constructed the poly command.


 key
to open the CUSTOM menu, the
key
to open the CUSTOM menu, the 


 key.
key.

 key
a number of times to get out of the menus displayed at the bottom of the screen.
key
a number of times to get out of the menus displayed at the bottom of the screen.