| To download,
use the link QUAD86 or the link QUAD85 . |

|
| To download,
use the link QUAD86 or the link QUAD85 . |

|

|
We start by pressing the
 key to obtain the menu of programs. Then we
use the
key to obtain the menu of programs. Then we
use the  key to move the menu to where
the QUAD program appears, as shown in Figure 1. key to move the menu to where
the QUAD program appears, as shown in Figure 1.
|

| We press the appropriate Function key,
for the display in Figure 1 that would be the  key,
to leave Figure 1
and produce the display on Figure 2. key,
to leave Figure 1
and produce the display on Figure 2. |

|
We press the  key again to execute the QUAD
program. Figure 3 shows the immediate result. The program asks for a value for
the coefficient A.
Since we are looking at the problem key again to execute the QUAD
program. Figure 3 shows the immediate result. The program asks for a value for
the coefficient A.
Since we are looking at the problem
 key. This is the condition shown in Figure 3.
Then we press key. This is the condition shown in Figure 3.
Then we press  to have the calculator accept our answer.
This will move us to Figure 4. to have the calculator accept our answer.
This will move us to Figure 4.
|

| The calculator requests the value of B.
We respond with   .
The calculator asks for the value fo C.
We press the .
The calculator asks for the value fo C.
We press the  key. This produces the image seen in Figure 4. key. This produces the image seen in Figure 4. |

| We leave Figure 4 by pressing the  key.
The calculator processes the information given and produces the result seen
in Figure 5. In particular, we see that the value of the discriminant is 4,
that there are two answers, and that those values
are key.
The calculator processes the information given and produces the result seen
in Figure 5. In particular, we see that the value of the discriminant is 4,
that there are two answers, and that those values
are |
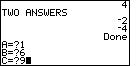
| Next we want to run the program to solve
 key.
Again the program requests the coeeficients, one at a time. We supply
those values to leave the screen as shown in Figure 6. key.
Again the program requests the coeeficients, one at a time. We supply
those values to leave the screen as shown in Figure 6.
|
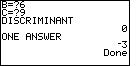
| We leave Figure 6 by pressing the  key.
The calculator processes the information given and produces the result seen
in Figure 7. In particular, we see that the value of the discriminant is 0,
that there is one answers, and that answer is key.
The calculator processes the information given and produces the result seen
in Figure 7. In particular, we see that the value of the discriminant is 0,
that there is one answers, and that answer is |

| Next we want to run the program to solve
 key.
Again the program requests the coeeficients, one at a time. We supply
those values to leave the screen as shown in Figure 8. key.
Again the program requests the coeeficients, one at a time. We supply
those values to leave the screen as shown in Figure 8. |

| We leave Figure 8 by pressing the  key.
The calculator processes the information given and produces the result seen
in Figure 9. In particular, we see that the value of the discriminant is -4,
and that there are no Real Number answers. key.
The calculator processes the information given and produces the result seen
in Figure 9. In particular, we see that the value of the discriminant is -4,
and that there are no Real Number answers. |

| Next we want to run the program to solve
 key.
Again the program requests the coeeficients, one at a time. We supply
those values to leave the screen as shown in Figure 10. key.
Again the program requests the coeeficients, one at a time. We supply
those values to leave the screen as shown in Figure 10. |

| We leave Figure 10 by pressing the  key.
The calculator processes the information given and produces the result seen
in Figure 11. In particular, we see that the value of the discriminant is 8,
that there are two answers, and that those values are key.
The calculator processes the information given and produces the result seen
in Figure 11. In particular, we see that the value of the discriminant is 8,
that there are two answers, and that those values are
|
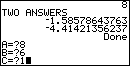
| Finally, we want to run the program to solve
 key.
Again the program requests the coeeficients, one at a time. We supply
those values to leave the screen as shown in Figure 12. key.
Again the program requests the coeeficients, one at a time. We supply
those values to leave the screen as shown in Figure 12. |

| We leave Figure 12 by pressing the  key.
The calculator processes the information given and produces the result seen
in Figure 13. In particular, we see that the value of the discriminant is 4,
that there are two answers, and that those values are key.
The calculator processes the information given and produces the result seen
in Figure 13. In particular, we see that the value of the discriminant is 4,
that there are two answers, and that those values are |
PRECALCULUS: College Algebra and Trigonometry
© 2000 Dennis Bila, James Egan, Roger Palay