| QUAD2, part 1 | QUAD2, part 2 |
 |
 |
The web page 208307.htm presents and describes a program, QUAD1, that performs the "quadratic formula" for solving certain quadratic equations of the form
| QUAD2, part 1 | QUAD2, part 2 |
 |
 |
A comparison of part 1 of the QUAD2 program with the QUAD1 program given on the earlier quad1.htm page, should confirm that the main part of the program is unchanged from one version to the other. The extra lines in QUAD2 are used to handle the case of the Complex Number answers. This is done by identifying, through examining the Discriminant, cases where the answer will be Complex, and retaining that information in the variable T. T will be used later in the program to format the output to include the imaginary number i for complex answers. Also, notice that the QUAD2 program calls (makes reference to) the TOSTR program in order to acheive a nicer looking output. TOSTR must be available on the calculator. The listing for the TOSTR program, was given on the 208304.htm page.
Naturally, one could enter the programs into a calculator. However, the TI-83 file for QUAD2 in is available at quad2.83p and the TI-83 file for TOSTR at tostr.83p. Depending upon your browser, you should be able to save the file to your disk and then transfer it via TI-Graphlink, assuming you have the program and the required cable.
We conclude this page with few sample runs of the TI-83 version of the QUAD2 program. We will be solving the following quadratic equations:
|
We open the PRGM menu by pressing the  key
and then moving, if need be, to find the QUAD2 program.
On the calculator used here the QUAD2 program is in position 8.
We can press the key
and then moving, if need be, to find the QUAD2 program.
On the calculator used here the QUAD2 program is in position 8.
We can press the
 key to select that program and to move to Figure 2. key to select that program and to move to Figure 2.
|

| All that has been accomplished is to paste the command
prgmQUAD2 onto the screen. We will have to press the
 key to actually start to run the program. key to actually start to run the program.
|
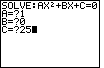
| In Figure 3 the program has started.
The calculator has asked for, and we have supplied, values for the
coefficients A, B, and C.
We have entered the value 1 for A,
0 for B and the value 25 for C.
These are the coefficients for
 to accept the
value for C and to move on with the program. to accept the
value for C and to move on with the program.
|

|
Figure 4 shows output from the calculator. It writes the word DISCRIMINANT
followed, on the next line, by
the value of the discriminant. Recall that the discriminant for
|
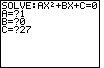
| The program was completed in Figure 4. To restart it, we press
 .
Figure 5 gives the data entry for the problem .
Figure 5 gives the data entry for the problem
|

| To accept our final value and continue the program we press
 .
Figure 6 gives the result. This time the discriminant has the value -108.
Because the discriminant is negative there will be two complex solutions.
The program goes on to show those solutions. .
Figure 6 gives the result. This time the discriminant has the value -108.
Because the discriminant is negative there will be two complex solutions.
The program goes on to show those solutions.
|
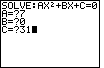
|
In Figure 7 we have restarted the program by pressing the  key. This time we are working on the problem
key. This time we are working on the problem
|

|
Pressing the  key to accept our last input value, the program
generates the information seen in Figure 8. In particular, we see that the value of the
discriminant is -868, that there are two answers, that the two answers are complex, and
it gives these values. Again, the program is "Done" running. key to accept our last input value, the program
generates the information seen in Figure 8. In particular, we see that the value of the
discriminant is -868, that there are two answers, that the two answers are complex, and
it gives these values. Again, the program is "Done" running.
|
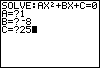
|
In Figure 9 we have restarted the program by pressing the  key. This time we are working on the problem
key. This time we are working on the problem
|

|
Again, we press  to contiue with the program. Figure 10 shows the discriminant
to be -36, that there are two complex answers, and the two answers. to contiue with the program. Figure 10 shows the discriminant
to be -36, that there are two complex answers, and the two answers.
|
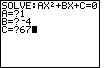
|
In Figure 11 we have started the program again, this time to solve the problem
|

| The program finds the discriminant, finds that there are two complex answers, gives those values. |

|
In Figure 13 we have started the program again, this time to solve the problem
|

|
We press the  key to leave Figure 13 and move to Figure 14.
Here we see that the value of the discriminant is -3920, and that there are two complex solutions,
and we are given the values of those answers. key to leave Figure 13 and move to Figure 14.
Here we see that the value of the discriminant is -3920, and that there are two complex solutions,
and we are given the values of those answers.
|
PRECALCULUS: College Algebra and Trigonometry
© 2000 Dennis Bila, James Egan, Roger Palay