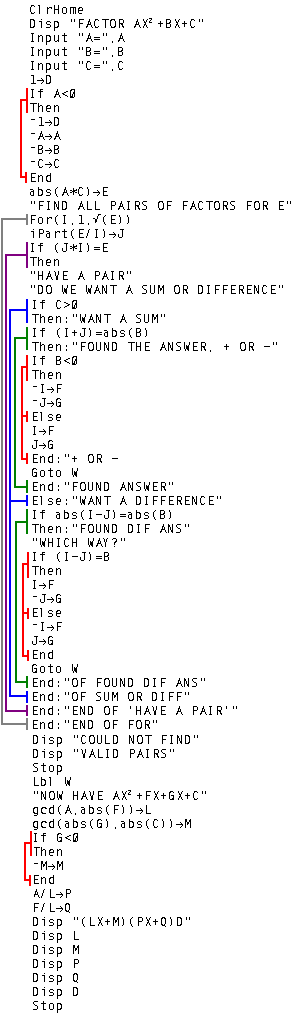
After working with the "split the middle term" scheme for factoring trinomials of the form

We start by clearing the screen and getting the three coefficients A, B, and C, from the user. Our goal will be to find F and G so that F*G=A*C and F+G=B. Then we can rewrite the polynomial as AX2 + FX + GX + C. Next we want to make sure that A is positive. We assume tht we will multiply the entire expressing by D. We start D as 1, but if A is negative, we set D to hold -1 and change the sign on every coefficient. We will multiply A times C, ignoring the sign of C, to get our goal product. Then, we will search for each pair of factors for that product. We need only look from 1 through the square root of E. If I goes into E exactly J times, then I and J are factors of E. However, there are different things to do if we are finding the sum or the difference of the factors. If C is positive then we want the sum, otherwise we will want the difference. We want the sum to be B, but B could be positive or negative. If B is negative, then both factors will be negative. If B is not negative, both factors will be positive. We have done all that we need to do, go to Lbl W for the next phase. The ELSE here is for the case where we want a Difference, not a Sum. In this case we just need to know if we can get the right difference. Therefore we need only compare the absolute values. There are only two possibilities, I-J=B or J-I=B. Choose the right one and set the values for F and G as indicated. We have done all that we need to do, go to Lbl W for the next phase. To get here we went through all of the factors of E and did not find one that produced the required sum of difference. Therefore, there is no integer answer. At Lbl W we have created F and G. Now we need to get the common factor for A and F and the common factor for G and C. This will give rise to the rest of the values in the answer. We have all the values. Display a template for the values and then the five values themselves.

Naturally, one could enter the program into a calculator. However, the file for the program in is available at trifact1.83p. Depending upon your browser, you should be able to save the file to your disk and then transfer it via TI-Graphlink, assuming you have the program and the required cable.

We conclude this page with few sample runs of the program:

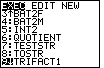
Figure 1	We open the PRGM menu by pressing the key and then moving, if need be, to find the TRIFACT1 program. The calculator used to generate Figure 1 has this program in position 9 of the list. Having highlighted the TRIFACT1 program, we can press the key to move to Figure 2.
Figure 2	All that has been accomplished is to paste the command prgmTRIFACT1 onto the screen. We will have to press the Having highlighted the TRIFACT1 program, we can press the key to actually start to run the program.
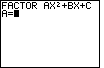
Figure 3	In Figure 3 the program has started. It has cleared the display and written the heading, FACTOR AX2+BX+C at the top. In addition, the calculator has printed the prompt A= and the calculator is waiting for our response.
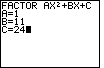
Figure 4	Not only did we supply the value 1 for A, Figure 4 shows that we have entered the value 11 for B and the value 24 for C. These are the coefficients for X2 + 11X + 24 The calculator is waiting for us to press to accept the value for C and to move on with the program.
Figure 5	Figure 5 shows the answer produced by the program. The template (LX+M)(PX+Q)D is displayed. Then the values for L, M, P, Q, and D are given. From this we can determine that the original problem X2 + 11X + 24 factors into (1X+8)(1X+3)1 where the final 1 is not needed. Thus, we obtain (X+8)(X+3)
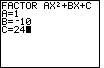
Figure 6	The program was completed in Figure 5. To restart it, we press . Figure 6 gives the data entry for the problem X2 - 10X + 24 Note the negative value for B, namely, -10.
Figure 7	Figure 7 shows the result, after entering the value for C and pressing . From these values we obtain a factoring of (1X-6)(1X-4)1 or (X-6)(X-4)
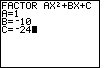
Figure 8	Figure 8 gives the data entry for the problem X2 - 10X - 24
Figure 9	Figure 9 shows the result, after entering the value for C and pressing . From these values we obtain a factoring of (1X-12)(1X+2)1 or (X-12)(X+2)
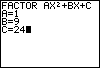
Figure 10	Figure 10 gives the data entry for the problem X2 + 9X + 24
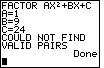
Figure 11	The program TRIFACT1 can not factor this trinomial using just integers. The message to that effect is displayed on the screen seen in Figure 11.
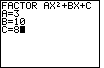
Figure 12	Figure 12 gives the data entry for the problem 3X2 + 10X + 8
Figure 13	Figure 13 shows the result, after entering the value for C and pressing . From these values we obtain a factoring of (1X+2)(3X+4)1 or (X+2)(3X+4)
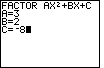
Figure 14	Figure 14 gives the data entry for the problem 3X2 + 2X - 8
Figure 15	Figure 15 shows the result, after entering the value for C and pressing . From these values we obtain a factoring of (1X+2)(3X-4)1 or (X+2)(3X-4)
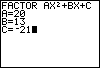
Figure 16	Figure 16 gives the data entry for the problem 20X2 + 13X - 21
Figure 17	Figure 17 shows the result, after entering the value for C and pressing . From these values we obtain a factoring of (5X+7)(4X-3)1 or (5X+7)(4X-3)

The TRIFACT1 program, given and illustrated above, produces output that asks the user to associate the numeric answers with the coefficients of a standard answer