Mathematical Relations
Introduction of Cartesian Products for Sets
The text and the detailed notes on sets page have presented some
basic ideas on sets. There have been examples of sets. We have listed sets and
in the detailed notes page we have presented descriptions of sets using
set-builder notation. Furthermore,
we have looked at two operations on sets, intersection
and union. These operations allow us to form a new set from
two existing sets. If we start with two sets, for example,
A={2,3,5,7}
B={4,5,6} the
we can form the union
A B={2,3,4,5,6,7}
and the intersection
A
B={2,3,4,5,6,7}
and the intersection
A B={5}
In both cases, the result is another set.
B={5}
In both cases, the result is another set.
Now we will present the Cartesian product of two sets. The symbol for the Cartesian product
is " " and we write
A
" and we write
A B and we read this as "A CROSS B", meaning
"find the Cartesian product on set A and set B."
But what is the answer? What is the new set formed by
A
B and we read this as "A CROSS B", meaning
"find the Cartesian product on set A and set B."
But what is the answer? What is the new set formed by
A B? The "set builder" notation for
the answer is
B? The "set builder" notation for
the answer is
A B={ (x,y) | x
B={ (x,y) | x A, y
A, y B}
which means that the answer is a set of things such as "(7,4)" because "(7,4)" satisfies
the set-builder definition. It is a pair of values, enclosed in parentheses and separated by a comma
where the first value is an element of set A and the second value is an element of set B.
The "set listing" of A
B}
which means that the answer is a set of things such as "(7,4)" because "(7,4)" satisfies
the set-builder definition. It is a pair of values, enclosed in parentheses and separated by a comma
where the first value is an element of set A and the second value is an element of set B.
The "set listing" of A B is
B is
A B={ B={ |
(2,4),(2,5),(2,6), |
| | (3,4),(3,5),(3,6), |
| | (5,4),(5,5),(5,6), |
| | (7,4),(7,5),(7,6)} |
The answer did not have to be written on four lines, it was merely convenient to do so, and it reveals
a systematic means for listing the elements of the Cartesian product.
The listing makes it clear that we can correctly write
(7,4) A
A B
An element of the Cartesian product of two sets, such as (7,4) above, is called an
"ordered pair", it is two values, the first drawn for the first set and the second drawn from
the second set, separated by a comma and enclosed in parentheses.
B
An element of the Cartesian product of two sets, such as (7,4) above, is called an
"ordered pair", it is two values, the first drawn for the first set and the second drawn from
the second set, separated by a comma and enclosed in parentheses.
We might note that both set union,  , and set intersection,
, and set intersection,
 , are commutative. It is always true that
, are commutative. It is always true that
A  B = B
B = B  A
and
A
A
and
A  B = B
B = B  A
However, the Cartesian product,
A
However, the Cartesian product,  , is not generally commutative. Except for the case where
set A equals set B,
A
, is not generally commutative. Except for the case where
set A equals set B,
A  B does not equal B
B does not equal B  A
In our example of the specific sets
A={2,3,5,7}
A
In our example of the specific sets
A={2,3,5,7}
B={4,5,6} we gave the listing for
A B above. The listing for
B
B above. The listing for
B A is
A is
B A={ A={ |
(4,2),(4,3),(4,5),(4,7), |
| | (5,2),(5,3),(5,5),(5,7), |
| | (6,2),(6,3),(6,5),(6,7)} |
These are quite different answers. We have the fact that
(7,4) A
A B
but (7,4)
B
but (7,4)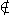 B
B A
and
(4,7)
A
and
(4,7)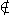 A
A B
but
(4,7)
B
but
(4,7) A
A B
B
We can form the Cartesian product of any two non-empty sets. In fact, we can form the
Cartesian Product of a set with itself. From the two sets,
A={2,3,5,7}
B={4,5,6} we could form
A A={ A={ |
(2,2),(2,3),(2,5),(2,7), | |
B B={ B={ |
(4,4),(4,5),(4,6), |
| |
(3,2),(3,3),(3,5),(3,7), | |
|
(5,4),(5,5),(5,6), |
| |
(5,2),(5,3),(5,5),(5,7), | |
|
(6,4),(6,5),(6,6)} |
| |
(7,2),(7,3),(7,5),(7,7)} | |
|
|
These examples have used finite sets A and B. But the definition of
Cartesian product does not restrict us to finite sets.
We could form W W for the set of whole numbers,
or Z
W for the set of whole numbers,
or Z Z for the integers, or
R
Z for the integers, or
R R for the set of real numbers.
R for the set of real numbers.
Relations as sets of Ordered Pairs
As noted in the book, a relation is a set of ordered pairs.
We know what an ordered pair looks like; it is two values, separated by comma
and surrounded by parentheses. Therefore,
{(3,4),(2,5),(2,6),(5,4),(7,5)}
is a relation. It is a set of ordered pairs. Of course, we know that we generated
ordered pairs by looking at the Cartesian product of two sets. We also know
that in each ordered pair, (x,y), the first value came from the first set and the
second value, y, came from the second set. For the relation
{(3,4),(2,5),(2,6),(5,4),(7,5)}
we can look at all of the first values and make a set of those values. In this example, that set
would be A={2,3,5,7}. And, we can find the set of all second values in each
ordered pair of the relation. In this example that is B={4,5,6}. We can then
find A B, which for this example is exactly the
set
B, which for this example is exactly the
set
A B={ B={ |
(2,4),(2,5),(2,6), |
| | (3,4),(3,5),(3,6), |
| | (5,4),(5,5),(5,6), |
| | (7,4),(7,5),(7,6)} |
Each ordered pair in our relation has a first value
that is in set A, and a second value that is in set B.
This must be true since we created
A by making the set of all first values and B by making a set of all second
values. Each ordered pair in the relation is an element of the set that is the relation.
Therefore, each ordered pair in the relation is also an element in the Cartesian
product of our sets A and B. That makes the relation a subset of the
Cartesian product of our sets A and B.
We have special names for the set of all first values and the set of all second values
of a relation. The set of all first values is called the Domain.
The set of all second values is called the Range. In the example that we have
been using, A is the Domain and B is the Range. The relation
is a subset of
Domain Range.
In addition, we have special names for the values in an ordered pair. The
first value is called the abscissa and the second is called the ordinate.
These are specific special names. The general term for the values in an ordered pair is
coordinates. Thus, the abscissa is the first coordinate
and the ordinate is the
second coordinate.
Range.
In addition, we have special names for the values in an ordered pair. The
first value is called the abscissa and the second is called the ordinate.
These are specific special names. The general term for the values in an ordered pair is
coordinates. Thus, the abscissa is the first coordinate
and the ordinate is the
second coordinate.
We have been using the sets
A={2,3,5,7}
B={4,5,6} .
From these sets we can form A B which becomes
the universal set. We can take any non-empty subset of A
B which becomes
the universal set. We can take any non-empty subset of A B
and that subset forms a relation because it is a set of ordered pairs.
We could produce a listing for any such relation.
{(3,4),(2,5),(2,6),(5,4),(7,5)} is an example of such a listing.
Sometimes there is some rule that allows us to describe a relation rather than to list it.
For example, we might look at the subset of A
B
and that subset forms a relation because it is a set of ordered pairs.
We could produce a listing for any such relation.
{(3,4),(2,5),(2,6),(5,4),(7,5)} is an example of such a listing.
Sometimes there is some rule that allows us to describe a relation rather than to list it.
For example, we might look at the subset of A B where
the sum of the letters in the names of the abscissa and ordinate is an even number. Thus,
(2,6) would be in this relation because there are 3 letters in the name "two" and there
are 3 letters in the name "six", and 3+3 is 6 which is an even number.
We could use set-builder
notation to describe the relation as
{(x,y)|x
B where
the sum of the letters in the names of the abscissa and ordinate is an even number. Thus,
(2,6) would be in this relation because there are 3 letters in the name "two" and there
are 3 letters in the name "six", and 3+3 is 6 which is an even number.
We could use set-builder
notation to describe the relation as
{(x,y)|x A, y
A, y B,
sum of letters in x and y is an even number}
or we could list the elements as
{(2,6),(3,6),(7,6),(5,4),(5,5)}.
Either way, the relation is a set of ordered pairs, and it is a subset of
A
B,
sum of letters in x and y is an even number}
or we could list the elements as
{(2,6),(3,6),(7,6),(5,4),(5,5)}.
Either way, the relation is a set of ordered pairs, and it is a subset of
A B. There are lots of different subsets
of A
B. There are lots of different subsets
of A B, and this relation is just one of them.
B, and this relation is just one of them.
Most of the time we are interested n relations where the "rule" that we use
to describe the relation is more mathematical. For example, we might take the
subset of A B where the sum of the abscissa and the
ordinate is 9. We could list this relation as {(3,6),(5,4)} or we could use set-builder
notation:
B where the sum of the abscissa and the
ordinate is 9. We could list this relation as {(3,6),(5,4)} or we could use set-builder
notation:
{(x,y)|x A, y
A, y B,
x + y = 9}
B,
x + y = 9}
We know that if we have sets A and B
then A B has A as the Domain and B as the Range.
B has A as the Domain and B as the Range.
{(x,y)|x A, y
A, y B,
x + y = 9}
especially when we understand that
x
B,
x + y = 9}
especially when we understand that
x A and y
A and y B.
Therefore, we quickly drop stating these requirements when they are understood.
We will simply write {(x,y)|x + y = 9}.
B.
Therefore, we quickly drop stating these requirements when they are understood.
We will simply write {(x,y)|x + y = 9}.
Graphing a Relation
We can represent a relation by a graph. For the most of our examples we will be using
numbers. However, let us start with a relation that has nothing to do with numbers.
The relation is
{(dog,br),(cat,bl),(bird,bl),(bird,br),(dog,red),(fish,bl)}
First, this is a relation because it is a set of ordered pairs. From the set we can
determine that the domain is the set
D={dog,cat,bird,fish}
and the range is the set
G={bl,br,red}.
We can graph this relation by placing the elements of the domain along the
bottom edge of the chart, and placing the elements of the range along the right
edge of the chart. Then, each element of the relation has an abscissa, the first value,
and an ordinate, the second value. We will put a mark on the graph directly above the
the domain value that is the same as the abscissa and directly across from the
range value that is the same as the ordinate.
Thus our graph would appear as
In the graph above, for the sake of spacing and appearance, the elements of the
domain, listed across the bottom, do not happen to be on consecutive vertical lines.
Furthermore, we only placed the elements of the domain along the bottom of the graph.
Let us consider another relation, one that uses numbers for the domain and the range.
The relation we will use is
{(0,10),(1,4),(3,0),(3,5),(9,0),(9,4),(9,10),(10,5)}
We could graph this relation as
Again, we placed the elements of the domain along the bottom and the elements of the
range along the side. The markers indicate the elements of the relation.
The problem with the graph above is that it seems unnatural. After all,
we know how to count and it seems strange to see the domain listed as 0, 1, 3, 9, and 10.
It would be more natural to have the bottom of the graph run 1, 2, 3, 4, and so on.
The same is true for the left side of the graph. For example, the following chart
has the same relation marked on it.
This is a much more natural graph. What we have lost is that we can no longer read the
domain from the list of items along the bottom, nor the range from the
labels along the left side. With the new graph we need to use the marks to reconstruct
the domain and the range. Now, just reading from the chart, the domain will be
all of the bottom values that have one or more marks above it. The range will be
all of the left values that have one or more marks across from it.
Let us use a new chart and we will construct the domain, the range, and the
relation from the chart.
The domain of this relation is {1,3,5,8} because those are the only values with marks above
them. The range is {1,2,3,4,7} because those are the only values across from the marks of
the relation. The relation is
{(1,7), (1,3), (3,4), (5,3), (5,7), (8,1), (8,2), (8,3), (8,4)}.
These new versions of graphs, where we have the graph marked off in regular intervals,
allow us to associate points with distance. It is even easier to do this if we have a starting
point. The graph below demonstrates our rectangular coordinate system. On that
graph we have marked the point (0,0), called the origin. We have also drawn
heavier vertical and horizontal lines through (0,0).
In addition, we have marked a point called D at (8,4) and a point
called E at (-6,10).
The horizontal line is called the x-axis and the vertical line is calld the y-axis.
These names are marked on the graph. That graph now represents the relation
{(0,0),(8,4),(-6,10)}.
The point D at (8,4) is 8 units to the right of the origin and it is
4 units above the origin. The 8 is the abscissa, the first value
in the ordered pair. It is giving us the distance to move, left or right,
from the origin. The 4 is the ordinate, the second value in the ordered
pair. It is giving us the distance to move, up or down, from the
origin. The point E at (-6,10) is 6 units
to the left of the origin
and 10 units above the origin.
Any point that we mark on the graph can be
located by giving the horizontal and vertical distances (and directions) from the origin.
Similarly, any ordered pair of values, (x,y), can be associated with a point on the
graph by locating that point x units horizontally from the origin and y units vertically
from the origin. For that reason, we refer to the abscissa, the first value in the
ordered pair, as the x-value or x-coordinate, and we refer to the ordinate, the second value
in the ordered pair, as the y-value or y-coordinate.
Let us look at another chart, this one with five points marked on it.
The question is: What are the ordered pairs represented by J, K, L, M, and N?
The answer is that J=(4,-2), K=(-2,3), L=(-6,-4), M=(3,-5), and N=(3,4). And the
relation represented by that chart is
{(4,-2), (-2,3),(-6,-4),(3,-5),(3,4)}
with a domain={4,-2,-6,3} and a range={-2,3,-4,-5,4}.
Graphing an Infinite Relation
The examples given above have had a finite Domain and Range. As a result,
we can list all the elements of the relation, and we can graph the relation as a set of points.
However, we can have relations that are defined with infinite sets. For example, we can have a
relation that is the set of ordered pairs, (x,y), such that x is a Whole number and y is always
one more than twice the value of x. The set-builder notation for this would be
{(x,y)| x W, y=2x+1}
and we could list the elements of the relation as
{ (0,1), (1,3), (2,5), (3,7), (4,9),... }
where the elipsis (the three dots) indicates that the pattern continues.
To show this on a graph, we can plot the points and put an arrow
on the point (4,9) to indicate that the pattern continues. This is done in the
graph below.
A similar situation would occur if the domain for the previous function is the set of integers.
The set-builder notation becomes
{(x,y)| x
W, y=2x+1}
and we could list the elements of the relation as
{ (0,1), (1,3), (2,5), (3,7), (4,9),... }
where the elipsis (the three dots) indicates that the pattern continues.
To show this on a graph, we can plot the points and put an arrow
on the point (4,9) to indicate that the pattern continues. This is done in the
graph below.
A similar situation would occur if the domain for the previous function is the set of integers.
The set-builder notation becomes
{(x,y)| x Z, y=2x+1}
However, with this change the pattern of the listing continues in both directions:
{ ..., (0,1), (1,3), (2,5), (3,7), (4,9),... }
and, to make the pattern even more clear, we could add another point or two with negative values,
giving
{ ..., (-2,-3), (-1,1), (0,1), (1,3), (2,5), (3,7), (4,9),... }
To show this on the graph we would add the new points and put an arrow at each end of the
points that have been plotted:
Note that the scale on the graph has been changed to accommodate the new values.
Z, y=2x+1}
However, with this change the pattern of the listing continues in both directions:
{ ..., (0,1), (1,3), (2,5), (3,7), (4,9),... }
and, to make the pattern even more clear, we could add another point or two with negative values,
giving
{ ..., (-2,-3), (-1,1), (0,1), (1,3), (2,5), (3,7), (4,9),... }
To show this on the graph we would add the new points and put an arrow at each end of the
points that have been plotted:
Note that the scale on the graph has been changed to accommodate the new values.
Graphing a Relation with a Real Number Domain
The example above used an infinite set, the Integers, for the domain of a relation.
We could use the Real numbers as the domain of a relation. For example, we could take the
relation
{(x,y)| x R, y=2x+1}
as the set-builder notation for the relation. We can not list the elements of the set
because we can not find a pattern that we can repeat to generate all of the Real numbers.
However, we know that all of the ordered pairs that we in the earlier relation will
be in this one. We will also have points such as (1.5,4), (1.9,4.8), (1.99,4.98).
When we graph this relation we will be generating all of the points on a line:
Note the arrows at the end of the line that represents the relation. It is possible, by limiting the
domain, for us to have a relation with a graph that has only one arrow. We could modify the relation that we
have been using so that it reads
{(x,y)| x
R, y=2x+1}
as the set-builder notation for the relation. We can not list the elements of the set
because we can not find a pattern that we can repeat to generate all of the Real numbers.
However, we know that all of the ordered pairs that we in the earlier relation will
be in this one. We will also have points such as (1.5,4), (1.9,4.8), (1.99,4.98).
When we graph this relation we will be generating all of the points on a line:
Note the arrows at the end of the line that represents the relation. It is possible, by limiting the
domain, for us to have a relation with a graph that has only one arrow. We could modify the relation that we
have been using so that it reads
{(x,y)| x R, x>-2, y=2x+1}
That will restrict the domain to Real numbers greater than -2. We will need to
graph a line that starts from (-2,-3) but does not include (-2,-3), and that continues
through points such as (-1,-1), (0,1), (1.5,4), and so on. Such a graph is given below:
Note the use of the small, open, circle at the point (-2,-3) to indicate that the
point is not in the relation. If the relation had been defined to include -2 in the
domain, then we would have used a filled circle at the point (-2,-3) to indicate that
we are specifically including that point in the picture.
R, x>-2, y=2x+1}
That will restrict the domain to Real numbers greater than -2. We will need to
graph a line that starts from (-2,-3) but does not include (-2,-3), and that continues
through points such as (-1,-1), (0,1), (1.5,4), and so on. Such a graph is given below:
Note the use of the small, open, circle at the point (-2,-3) to indicate that the
point is not in the relation. If the relation had been defined to include -2 in the
domain, then we would have used a filled circle at the point (-2,-3) to indicate that
we are specifically including that point in the picture.
Graphing a Step Relation
Let us try one more relation. In this case, we will look at a relation
that has a domain restriced to the Real number values from -3 to 4, inclusive. The
relation is defined as
{(x,y)|x R, -3<=x<=3, y=int(x)}
where "int(x)" means "the largest integer less than or equal to x. For example, the
int(2) is 2, the int(2.3) is 2, and the int(2.99) is still 2. However, int(3.01) is 3
and the int(-2.2) is -3. The following graph represents this relation.
Depending on your browser, the line segments, for example the line segment from (-3,-3) to (-2,-3)
may be difficult to see, but it is there. Becuase the
graph of the relation stays flat for a while and then it jumps up to a new
level, we call this a "step relation". (It looks somewhat like the side view of
a set of steps.)
R, -3<=x<=3, y=int(x)}
where "int(x)" means "the largest integer less than or equal to x. For example, the
int(2) is 2, the int(2.3) is 2, and the int(2.99) is still 2. However, int(3.01) is 3
and the int(-2.2) is -3. The following graph represents this relation.
Depending on your browser, the line segments, for example the line segment from (-3,-3) to (-2,-3)
may be difficult to see, but it is there. Becuase the
graph of the relation stays flat for a while and then it jumps up to a new
level, we call this a "step relation". (It looks somewhat like the side view of
a set of steps.)
We can drop the lone point at (3,3) and move the lines of the relation off of the grid lines
by changing the relation to
{(x,y)|x R, -3<=x<3, y=int(x)+1/2}
Note that the domain has been changed to not include 3. That will eliminate
that single point at the top of the graph. Adding 1/2 to each value of y will
shift the graph up by 1/2 and move it off of the grid lines.
The following graph represents this relation.
This should be a more clear picture of the relation.
R, -3<=x<3, y=int(x)+1/2}
Note that the domain has been changed to not include 3. That will eliminate
that single point at the top of the graph. Adding 1/2 to each value of y will
shift the graph up by 1/2 and move it off of the grid lines.
The following graph represents this relation.
This should be a more clear picture of the relation.
PRECALCULUS: College Algebra and Trigonometry
© 2000 Dennis Bila, James Egan, Roger Palay
 B={2,3,4,5,6,7}
B={2,3,4,5,6,7}  B={2,3,4,5,6,7}
B={2,3,4,5,6,7}  B={5}
B={5} " and we write
A
" and we write
A B and we read this as "A CROSS B", meaning
"find the Cartesian product on set A and set B."
But what is the answer? What is the new set formed by
A
B and we read this as "A CROSS B", meaning
"find the Cartesian product on set A and set B."
But what is the answer? What is the new set formed by
A B? The "set builder" notation for
the answer is
B? The "set builder" notation for
the answer is B={ (x,y) | x
B={ (x,y) | x A, y
A, y B}
B}
 B is
B is
 B={
B={ A
A B
B
 , and set intersection,
, and set intersection,
 , are commutative. It is always true that
, are commutative. It is always true that
 B = B
B = B  A
A  B = B
B = B  A
A  , is not generally commutative. Except for the case where
set A equals set B,
, is not generally commutative. Except for the case where
set A equals set B,
 B does not equal B
B does not equal B  A
A  B above. The listing for
B
B above. The listing for
B A is
A is
 A={
A={ A
A B
B
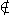 B
B A
A
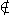 A
A B
B
 A
A B
B
 A={
A={ B={
B={ W for the set of whole numbers,
or Z
W for the set of whole numbers,
or Z Z for the integers, or
R
Z for the integers, or
R R for the set of real numbers.
R for the set of real numbers.
 B, which for this example is exactly the
set
B, which for this example is exactly the
set
 B={
B={ Range.
Range.
 B which becomes
the universal set. We can take any non-empty subset of A
B which becomes
the universal set. We can take any non-empty subset of A B
and that subset forms a relation because it is a set of ordered pairs.
We could produce a listing for any such relation.
B
and that subset forms a relation because it is a set of ordered pairs.
We could produce a listing for any such relation.
 B where
the sum of the letters in the names of the abscissa and ordinate is an even number. Thus,
(2,6) would be in this relation because there are 3 letters in the name "two" and there
are 3 letters in the name "six", and 3+3 is 6 which is an even number.
We could use set-builder
notation to describe the relation as
B where
the sum of the letters in the names of the abscissa and ordinate is an even number. Thus,
(2,6) would be in this relation because there are 3 letters in the name "two" and there
are 3 letters in the name "six", and 3+3 is 6 which is an even number.
We could use set-builder
notation to describe the relation as
 A, y
A, y B,
sum of letters in x and y is an even number}
B,
sum of letters in x and y is an even number} B. There are lots of different subsets
of A
B. There are lots of different subsets
of A B, and this relation is just one of them.
B, and this relation is just one of them.
 B where the sum of the abscissa and the
ordinate is 9. We could list this relation as {(3,6),(5,4)} or we could use set-builder
notation:
B where the sum of the abscissa and the
ordinate is 9. We could list this relation as {(3,6),(5,4)} or we could use set-builder
notation:
 A, y
A, y B,
x + y = 9}
B,
x + y = 9} B has A as the Domain and B as the Range.
B has A as the Domain and B as the Range.
 A, y
A, y B,
x + y = 9}
B,
x + y = 9} A and y
A and y B.
Therefore, we quickly drop stating these requirements when they are understood.
We will simply write
B.
Therefore, we quickly drop stating these requirements when they are understood.
We will simply write  W, y=2x+1}
W, y=2x+1} Z, y=2x+1}
Z, y=2x+1} R, y=2x+1}
R, y=2x+1} R, x>-2, y=2x+1}
R, x>-2, y=2x+1} R, -3<=x<=3, y=int(x)}
R, -3<=x<=3, y=int(x)} R, -3<=x<3, y=int(x)+1/2}
R, -3<=x<3, y=int(x)+1/2}