This page is a listing of the main topics related to sets.
| Definition of a Set
| A set is a collection of objects or
things or even concepts, called elements. In a real sense, a set is a group of
things where we have some way to determine if something is either in the group or not
in the group. We might be able to write out the names of all the elements of the set.
If we can do that, then someone else can look at our list of elements and can determine
if something is or is not in our set. For example, I might tell you that I am thinking of a set
whose members are the colors red, blue, and yellow. My set has three elements. You can
read the list of those elements and you immediately know that "blue" is in the set and that
the color "purple" is not in the set.
Alternatively, we may describe a set by giving a rule for determining iof something is a
member of the set. For example, I might tell you
that I am thinking of the set of all counting number whose English names
are exactly three letters long. It is not immediately clear just how many
elements are in this set, but we can use the rule to test out different
possible values. The number "10" is in the set because "ten" satisfies the rule, it has exactly three
letters in it. On the other hand, the number "8" is not in the set
because "eight" has five, not three, letters in it. If we think about the counting numbers
we can eventually change the rule into a list of the numbers "1", "2", "6", and "10".
An interesting consequence of our definition of a set is that something is either an element of the
set or it is not an element of the set. Furthermore, if something is an element, then it is only
listed one time in the set. That is, we do not repeat elements in a set.
|
| Listing a set
| Gives the list of elements of the set, separated by commas,
enclosed in braces, as in
{4,6,8,10} as a set.
Notice that there is no order to the elements of a set. The set given as
{4,6,8,10} is the same as the set given as {6,10,4,8} which is the same as
the set given as {8,4,6,10}.
However, even though the elements of the set can appear in any order, there
are times that we find it convenient to list the elements in a specific order.
If a set is large and if its elements form some pattern, then we can use
three dots (called an ellipsis) to indicate that
the pattern continues either to a terminating few elements, as in
{3,6,9,12,...,57,60}, or forever, as in {1,4,9,16,25,36,...}.
The ellipsis can be used at either side, or on both
sides of the pattern. Threfore, we understand
{1, 3, 5, 7, 9, ...} to continue with 11, 13, 15, 17, and so on.
And we understand
{..., 5, 7, 9, 11} to contain the numbers 3, 1, -1, -3, and so on, in addition to the
numbers listed, 5, 7, 9, and 11. And, we understand
{ ..., 1/8, 1/4, 1/2, 1, 2, 4, 8, ... }
to contain values such as 1/16, 1/32, 1/64, and so on, as well as 16, 32, 64, 128, and so on.
As noted above, the ellipsis can be used in the middle of a listing in order to shorten
the list. An example of this would be
{31, 32, 33, 34, ..., 91, 92, 93}
where the ellipsis saves us from having to write out the numbers from 35 through 90.
|
| Set-builder notation.
| Specifies the elements of a set by giving a rule that is used
to determine if something is an element of the set, as in
{ x | x is a registered student in a WCC math class on April 7, 1998}
where the vertical bar, "|", is read as "such that". Thus the set described above is
read as The set of all things "x" such that "x"
is a registered student in a WCC math class on April 7, 1998.
The set-builder notation has both advantages and disadvanages over the
"listing" method for defining a set. With the set-buildeer notation
we need only state a rule that allows us to test to see if something is or is not
an element of the set. The example given above,
{ x | x is a registered student in a WCC math class on April 7, 1998}
is just such a rule. The advantage is that we do not hve to list all of the elements of
the set. For this example, that list would include over 2000 people. Rather than
the long list, we have a short rule. Furthermore, by stating the rule we are
conveying the "organizing concept" behind the set. If we had written the list of
over 2000 names it would not be clear, from the list, why someone is on the list and
why someone else is not.
The fact that the set-builder reveals the "organizing concept" behind the set
makes this form appealing.
The disadvantage of set-builder notation is that it relies on our language and
on our understanding of that language to apply the rule for set membership. For example,
there is some room for disagreement about the meaning of even such a simple statement as
is a registered student in a WCC math class on April 7, 1998
What if a student drops a math class at 3:30 on April 7? Is that student registered or not on April 7?
What is a student enrolls on April 7? What if a student is registered for a non-credit Math
class? What do we do with students who are registered for a math class but where that class only met during
the first half of the term, and therefore, it was over before March?
Thus, even though the intention of the set-builder notation may have been clear,
it is possible to raise questions about the rule. This is different from the set listing method.
There, for the most part, it is absolutely clear what is and is not a member of the set.
|
| Naming sets
| We often use capital letters to name a set, as in
B={4,5,6,7}. One problem with this is that we quickly run out of capital letters.
Therefore, we end up reusing letters from problem to problem. Whenever we make reference to
a set B you need to look back within the problem or the text to find out just
what set named B we are using.
|
| Set equality
| Two sets are equal if they have exactly the same elements.
As you might expect, we use the equals symbol, "=", to denote set equality.
Therefore, the statement A=B is read
as "the set A is equal to the set B", meaning that
the two sets have exactly the same elements.
|
| Subsets
| Set A is a subset of set B if every element of A is also an
element of B. We use the symbol 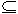 to
indicate "is a subset". Thus, A to
indicate "is a subset". Thus, A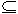 B
is read as "A is a subset of B".
Notice that if A B
is read as "A is a subset of B".
Notice that if A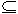 B then
it is possible that A=B. If A=B then certainly every element of A
must also be an element of B. But that is the definition of being a subset. Therefore,
A is a subset of B. Of course, if A=B, then every element of B is also an element
of A. Therefore, it is also true that B B then
it is possible that A=B. If A=B then certainly every element of A
must also be an element of B. But that is the definition of being a subset. Therefore,
A is a subset of B. Of course, if A=B, then every element of B is also an element
of A. Therefore, it is also true that B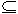 A. A.
The symbol 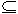 for "is a subset of" uses the lower
line to remind us that the two sets could be equal. for "is a subset of" uses the lower
line to remind us that the two sets could be equal.
We might notice that if A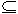 B
and B B
and B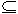 A then it must be true
that A=B. In many cases, when we want to prove that two sets are equal, we instead prove
that the first set is a subset of the second, and that the second is a
subset of the first. A then it must be true
that A=B. In many cases, when we want to prove that two sets are equal, we instead prove
that the first set is a subset of the second, and that the second is a
subset of the first.
We use the related symbol 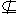 to mean
"is not a subset of". If we say that D to mean
"is not a subset of". If we say that D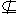 E
we are saying that D is not a subset of E.
In particular, this means that there must be at least one element of D that is not in E. E
we are saying that D is not a subset of E.
In particular, this means that there must be at least one element of D that is not in E.
|
| Proper Subsets
| Set A is a proper subset of set B
if A is a subset of B and
if B has at least one element that is not in A. We use the symbol
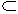 to
indicate "is a proper subset". Thus, A to
indicate "is a proper subset". Thus, A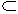 B
is read as "A is a proper subset of B". B
is read as "A is a proper subset of B".
We use the related symbol 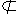 to mean
"is not a proper subset of". If we say that D to mean
"is not a proper subset of". If we say that D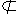 E
we are saying that D is not a proper subset of E.
There are two ways for set D to not be a proper subset of set E.
First, there may be at least one element of D that is not in E.
Second, D would not be a proper subset of E
if D=E. Either approach could be true. E
we are saying that D is not a proper subset of E.
There are two ways for set D to not be a proper subset of set E.
First, there may be at least one element of D that is not in E.
Second, D would not be a proper subset of E
if D=E. Either approach could be true.
|
| Empty Set or Null Set
| There is a special set called the Empty set or the Null set. It is the
set with no elements. We use two different symbols for the empty set.
One is braces with nothing between them, as in { }.
The other symbol used to represent the empty set is 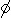 .
Note that the empty set is a subset of every set because every
element in the empty set (and there are none) is also an element of the other set. Thus,
for any set A we can write .
Note that the empty set is a subset of every set because every
element in the empty set (and there are none) is also an element of the other set. Thus,
for any set A we can write
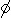 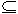 A.
Either symbol, { } or A.
Either symbol, { } or 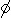 , can be used to
represent the empty or null set.
However, note that the set { , can be used to
represent the empty or null set.
However, note that the set {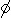 } is not the
empty set. Rather { } is not the
empty set. Rather {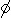 } is a set with one
element, and that element is the empty set. } is a set with one
element, and that element is the empty set.
|
| Universal set
| One might expect the universal set to be the set of everything, the set with
every possible element in it, just as the empty set is the set with no elements. Although we
could do this, it is better for us to define the Universal set as the set of all things under
current consideration. This means that the Universal set changes from problem to problem,
but it also means that the Universal set is reasonably small and well defined for each problem.
We use the capital letter U to represent the Universal set.
|
| Complement of a set.
| If the Universal set is the set of all the elements under consideration, and
A is a set of some of those elements, then the set of all elements in the Universal set that are
not in A is called the complement of A, and is denoted as A'.
This is an important concept. It means that for any universal set, any subset, A, of the universal set
really divides the universal set into two subsets, A and A'. Furthermore, an element is either in A or
it is in A', it can not be in both of them at the same time.
|
| Is an element of
| We use the symbol  to represent
"is an element of". Thus, for the set A={dog,bird,cat,horse,cow, mouse} we could write
cow to represent
"is an element of". Thus, for the set A={dog,bird,cat,horse,cow, mouse} we could write
cow  A
to say "cow is an element of A. A
to say "cow is an element of A.
|
| Is not an element of
| We use the symbol 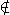 to represent
"is not an element of". Thus, for the set A={dog,bird,cat,horse,cow, mouse} we could write
rat to represent
"is not an element of". Thus, for the set A={dog,bird,cat,horse,cow, mouse} we could write
rat 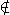 A
to say "rat is not an element of A. A
to say "rat is not an element of A.
|
| Intersection
| The intersection of two sets is a new set that has all of the elements that are
common to the original two sets. That is, to be in the Intersection, an element must be in both
of the original sets. We use the symbol  to mean "intersect"
and we write A to mean "intersect"
and we write A B to say A intersect B. If
A={2,4,6,8,10,12,14,16} and B={3,6,9,12,15,18,21,24,27} then
A B to say A intersect B. If
A={2,4,6,8,10,12,14,16} and B={3,6,9,12,15,18,21,24,27} then
A B={6,12}. B={6,12}.
|
| Disjoint Sets
| Two sets are said to be disjoint if the intersection of the two sets is the
empty set. In symbols, if
A B= B=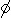 the A and B are called disjoint.
It should be clear that A and A' (the complement of A) are always disjoint.
the A and B are called disjoint.
It should be clear that A and A' (the complement of A) are always disjoint.
|
| Mutually disjoint
| For more than two sets, if each pair of sets is disjoint, then the sets are said to be
mutually disjoint.
|
| Union
| The union of two sets is a new set that has all of the elements that are
elements of either of the original two sets. That is, to be in the union, an element must be in one or
the other, or both,
of the original sets.
We use the symbol 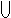 to mean "union"
and we write A to mean "union"
and we write A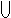 B to say A union B. If
A={2,4,6,8,10,12,14,16} and B={3,6,9,12,15,18,21,24,27} then
A B to say A union B. If
A={2,4,6,8,10,12,14,16} and B={3,6,9,12,15,18,21,24,27} then
A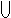 B={2,3,4,6,8,9,10,12,14,15,16,18,21,24,27}.
Also, note that for A B={2,3,4,6,8,9,10,12,14,15,16,18,21,24,27}.
Also, note that for A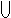 A'=U. A'=U.
|
| Venn Diagrams
| A Venn diagram is a picture that shows the relationship between sets.
In general we use a rectangle to represent the Universal set for the problem, and we
show various sets (subsets of the Universal set) as cirlces within the rectangle.
If two circles overlap, then the two sets have a non-empty intersection. If two circles do
not overlap, then the two sets are disjoint. If one circle is entirely inside another, then
the first set is a subset (in fact a proper subset) of the second.
|
| Cardinality of a set
| The cardinality of a set is the number of elements in the set.
We use the notation n(A) to represent the "cardinality of set A". If
A={2,4,6,8,10,12,14,16} and B={3,6,9,12,15,18,21,24,27} then n(A)=8 and n(B)=9.
|
| Finite sets
| To most of us it is pretty clear that the set {3, 4, 5, 6} is finite. After all,
it has just 4 elements. The set {2, 4, 6, 8, 10, ..., 98, 100}
is finite since it has exactly 50 elements.
The set {2, 4, 6, 8, 10, ..., 996, 998, 1000} is finite; it has exaclty 500 elements.
A set is finite if we could theoretically count the elements and end our count.
Consider the following situation.
We go to our local food store and we buy one pound box of salt.
Now that we have a specific box of salt, we can look at the
the set of all grains of salt in the box.
Clearly there is a huge number of grains of salt
in that box. I would not want to have to count them. But I could. And if I did, I would arrive a
some specific number of grains of salt in the box. Therefore, the set of all grains of salt
in that box is a finite set. If I bought a case of boxes of salt, then the
set of grains of salt that I
bought would be extremely large, but still finite.
In fact, the set of grains of salt in all the boxes of salt in all the
kitchens in all the houses in all of Washtenaw County at this moment, is a finite set. Now,
there is no way that we can stop time and gather up all the boxes of salt in
all the kitches in all the houses in all of Washtenaw County so that we can actually count
the grains of salt, but theoretically we could do this, and if we did we could count
the grains and at some point we would have counted each grain and we could stop. Therefore,
our set is finite.
|
| Infinite sets
| A set that has an unlimited number of elements is called an infinite set.
For example, the set of all even counting numbers, {2, 4, 6, 8, 10, ...} is infinite. It
does not stop. The set of all numbers that use the character 7 is infinite. It has elements
such as 7, 17, 27, 70, 71, 234789, and 7827927 in it, along with an endless collection of
other numbers.
Strangely enough, there are very few infinite sets in the real world. Most of the inifinte sets that
we will deal with are sets of numbers.
|
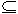 to
indicate "is a subset". Thus, A
to
indicate "is a subset". Thus, A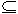 B
is read as "A is a subset of B".
Notice that if A
B
is read as "A is a subset of B".
Notice that if A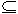 B then
it is possible that A=B. If A=B then certainly every element of A
must also be an element of B. But that is the definition of being a subset. Therefore,
A is a subset of B. Of course, if A=B, then every element of B is also an element
of A. Therefore, it is also true that B
B then
it is possible that A=B. If A=B then certainly every element of A
must also be an element of B. But that is the definition of being a subset. Therefore,
A is a subset of B. Of course, if A=B, then every element of B is also an element
of A. Therefore, it is also true that B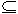 A.
A.
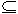 for "is a subset of" uses the lower
line to remind us that the two sets could be equal.
for "is a subset of" uses the lower
line to remind us that the two sets could be equal. 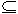 B
and B
B
and B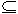 A then it must be true
that A=B. In many cases, when we want to prove that two sets are equal, we instead prove
that the first set is a subset of the second, and that the second is a
subset of the first.
A then it must be true
that A=B. In many cases, when we want to prove that two sets are equal, we instead prove
that the first set is a subset of the second, and that the second is a
subset of the first.
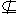 to mean
"is not a subset of". If we say that D
to mean
"is not a subset of". If we say that D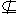 E
we are saying that D is not a subset of E.
In particular, this means that there must be at least one element of D that is not in E.
E
we are saying that D is not a subset of E.
In particular, this means that there must be at least one element of D that is not in E.
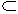 to
indicate "is a proper subset". Thus, A
to
indicate "is a proper subset". Thus, A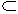 B
is read as "A is a proper subset of B".
B
is read as "A is a proper subset of B".
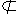 to mean
"is not a proper subset of". If we say that D
to mean
"is not a proper subset of". If we say that D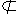 E
we are saying that D is not a proper subset of E.
There are two ways for set D to not be a proper subset of set E.
First, there may be at least one element of D that is not in E.
Second, D would not be a proper subset of E
if D=E. Either approach could be true.
E
we are saying that D is not a proper subset of E.
There are two ways for set D to not be a proper subset of set E.
First, there may be at least one element of D that is not in E.
Second, D would not be a proper subset of E
if D=E. Either approach could be true.
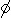 .
Note that the empty set is a subset of every set because every
element in the empty set (and there are none) is also an element of the other set. Thus,
for any set A we can write
.
Note that the empty set is a subset of every set because every
element in the empty set (and there are none) is also an element of the other set. Thus,
for any set A we can write
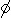
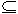 A.
Either symbol, { } or
A.
Either symbol, { } or 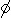 , can be used to
represent the empty or null set.
However, note that the set {
, can be used to
represent the empty or null set.
However, note that the set {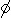 } is not the
empty set. Rather {
} is not the
empty set. Rather {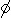 } is a set with one
element, and that element is the empty set.
} is a set with one
element, and that element is the empty set.
 to represent
"is an element of". Thus, for the set A={dog,bird,cat,horse,cow, mouse} we could write
to represent
"is an element of". Thus, for the set A={dog,bird,cat,horse,cow, mouse} we could write  A
A 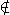 to represent
"is not an element of". Thus, for the set A={dog,bird,cat,horse,cow, mouse} we could write
to represent
"is not an element of". Thus, for the set A={dog,bird,cat,horse,cow, mouse} we could write 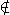 A
A  to mean "intersect"
and we write A
to mean "intersect"
and we write A B to say A intersect B. If
A={2,4,6,8,10,12,14,16} and B={3,6,9,12,15,18,21,24,27} then
A
B to say A intersect B. If
A={2,4,6,8,10,12,14,16} and B={3,6,9,12,15,18,21,24,27} then
A B={6,12}.
B={6,12}.
 B=
B=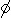 the A and B are called disjoint.
It should be clear that A and A' (the complement of A) are always disjoint.
the A and B are called disjoint.
It should be clear that A and A' (the complement of A) are always disjoint.
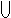 to mean "union"
and we write A
to mean "union"
and we write A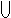 B to say A union B. If
A={2,4,6,8,10,12,14,16} and B={3,6,9,12,15,18,21,24,27} then
A
B to say A union B. If
A={2,4,6,8,10,12,14,16} and B={3,6,9,12,15,18,21,24,27} then
A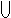 B={2,3,4,6,8,9,10,12,14,15,16,18,21,24,27}.
Also, note that for A
B={2,3,4,6,8,9,10,12,14,15,16,18,21,24,27}.
Also, note that for A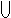 A'=U.
A'=U.