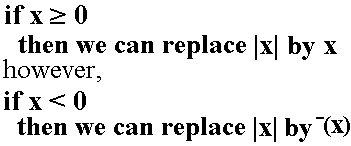
The problem is given as
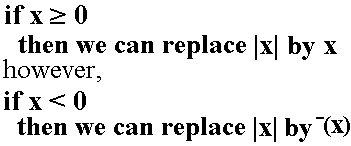
We do not know if 6x–1 is non-negative or negative. Therefore we divide the problem into two cases, one where 6x–1 is non-negative and one where 6x–1 is negative.
Case 1: 6x–1 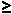 0 0 |
Case 2: 6x–1 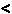 0 0 | ||||||||
In this case we know that 6x–1 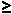 0.
First we note that this means that 0.
First we note that this means that 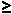 1 1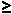 1/6. 1/6.
|
In this case we know that 6x–1 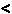 0.
First we note that this means that 0.
First we note that this means that 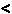 1 1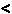 1/6. 1/6.
|
The table above produces the answers x=1/2 and x=– 1/2. The table represents a general soltuion to such problems in that it divides the problem into numerous cases such that we can replace the absolute value expressions with non-absolute value expressions. As a small note, the length and complexity of the table comes from the extensive commentary placed into it.
PRECALCULUS: College Algebra and Trigonometry
© 2000 Dennis Bila, James Egan, Roger Palay