Absolute Value

Our textbook follows the usual approaches to absolute value. There is nothing wrong with these approaches. However, it has been our experience that students have some difficulty with absolute value. Therefore, this page will present the topic again, with a slightly different twist.

The usual definition of absolute value looks like

Although this is a completely accurate, even elegant, definition, it does not seem like it helps students with absolute value problems. Let us consider an alternative (though equivalent) definition:

This definition does not look as nice as does the previous definition. However, this definition tells us how to solve problems that have absolute values in them. In particular, we use this definition to change problems from ones that have absolute values into new problems that do not have absolute values. Let us look at a number of examples.

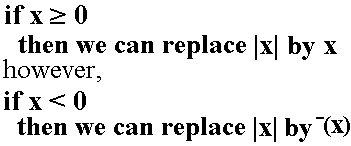
Problem 1	Solution
Find: \| 7 \|	Since 70, we replace \| 7 \| by 7 therefore, the answer is 7.

Problem 2	Solution
Find: \| ^–5 \|	Since ^–50, we replace \| ^–5 \| by ^–( ^–5 ) but, the value of ^–( ^–5 ) is 5 therefore, the answer is 5.

Problem 3

Solution

Find: | x | = 12

We do not know if x is negative, or non-negative.
We need to know this if we are going to use our definition.
We will break the problem into two cases, one where
x is negative, and one where x is non-negative.

Case 1: x 0	Case 2: x 0
For this case we know x0, therefore, we replace \| x \| by ^–(x) this gives ^–(x) = 12 which we solve to get x = ^–12 therefore, the answer is ^–12. Note that ^–12 is indeed a possible answer for this case.	For this case we know x0, we replace \| x \| by x to get x = 12 therefore, the answer is 12. Note that 12 is indeed a possible answer for this case.

Putting the two cases together, we have the solution is the set
{ ^–12, 12 }

Problem 4

Solution

Find: | x | = ^–7

Case 1: x 0	Case 2: x 0
For this case we know x0, therefore, we replace \| x \| by ^–(x) this gives ^–(x) = ^–7 which we solve to get x = 7 therefore, the answer, for this case, is 7. Note that 7 is not a possible answer for this case. Therefore, there is no possible answer for this case.	For this case we know x0, we replace \| x \| by x to get x = ^–7 therefore, the answer, for this case, is ^–7 . Note that 7 is not a possible answer for this case. Therefore, there is no possible answer for this case.

Putting the two cases together, we have the solution is the empty set
{ }

Problem 5

Solution

Find: | x + 8 | = 12

We do not know if x + 8 is negative, or non-negative.
We need to know this if we are going to use our definition.
We will break the problem into two cases, one where
x + 8 is negative, and one where x + 8 is non-negative.

Case 1: x+8 0
which means, x ^–8

Case 2: x+8 0
which means, x ^–8

For this case we know x+80,
therefore, we replace | x + 8 | by ^–(x+8)
this gives ^–(x+8) = 12
which is the same as (^–1)(x+8) = 12
which yields (^–1)x + (^–1)8 = 12
or, simplifying, ^–x = 20
which we solve to get x = ^–20
therefore, the answer is ^–20.
Note that ^–20 is indeed a possible answer for this case since we know that x ^–8 for this case.

For this case we know x+80,
we replace | x + 8 | by x + 8
to get x + 8 = 12
which is x = 4
therefore, the answer is 4.
Note that 4 is indeed a possible answer for this case, since we know that x ^–8 for this case.

Putting the two cases together, we have the solution is the set
{ ^–20, 4 }

Problem 6

Solution

Find: | x + 13 | = 6

We do not know if x + 13 is negative, or non-negative.
We need to know this if we are going to use our definition.
We will break the problem into two cases, one where
x + 13 is negative, and one where x + 13 is non-negative.

Case 1: x+13 0
which means, x ^–13

Case 2: x+13 0
which means, x ^–13

For this case we know x+130,
therefore, we replace | x + 13 | by ^–(x+13)
this gives ^–(x+13) = 6
which is the same as (^–1)(x+13) = 6
which yields (^–1)x + (^–1)13 = 6
or, simplifying, ^–x = ^–19
which we solve to get x = ^–19
therefore, the answer is ^–19.
Note that ^–19 is indeed a possible answer for this case since we know that x ^–13 for this case.

For this case we know x+130,
we replace | x + 13 | by x + 13
to get x + 13 = 6
which is x = ^–7
therefore, the answer is ^–7.
Note that ^–7 is indeed a possible answer for this case, since we know that x ^–13 for this case.

Putting the two cases together, we have the solution is the set
{ ^–19, ^–7 }

Problem 7

Solution

Find: | x – 9 | = 4

We do not know if x – 9 is negative, or non-negative.
We need to know this if we are going to use our definition.
We will break the problem into two cases, one where
x – 9 is negative, and one where x – 9 is non-negative.

Case 1: x–9 0
which means, x 9

Case 2: x–9 0
which means, x 9

For this case we know x–90,
therefore, we replace | x – 9 | by ^–(x–9)
this gives ^–(x–9) = 4
which is the same as (^–1)(x–9) = 4
which yields (^–1)x – (^–1)9 = 4
or, simplifying, ^–x + 9 = 4
or, simplifying, ^–x = ^–5
which we solve to get x = 5
therefore, the answer is 5.
Note that 5 is indeed a possible answer for this case since we know that x 9 for this case.

For this case we know x–90,
we replace | x – 9 | by x – 9
to get x – 9 = 4
which is x = 13
therefore, the answer is 13.
Note that 13 is indeed a possible answer for this case, since we know that x 9 for this case.

Putting the two cases together, we have the solution is the set
{ 5, 13 }

Problem 8

Solution

Find: | 3x + 5 | = 28

We do not know if 3x + 5 is negative, or non-negative.
We need to know this if we are going to use our definition.
We will break the problem into two cases, one where
3x + 5 is negative, and one where 3x + 5 is non-negative.

Case 1: 3x+5 0
which means, 3x ^–5
which means, x ^–5/3

Case 2: 3x+5 0
which means, 3x ^–5
which means, x ^–5/3

For this case we know 3x+50,
therefore, we replace | 3x + 5 | by ^–(3x+5)
this gives ^–(3x+5) = 28
which is the same as (^–1)(3x+5) = 28
which yields (^–1)3x + (^–1)5 = 28
or, simplifying, ^–3x = 33
which we solve to get x = ^–11
therefore, the answer is ^–11.
Note that ^–11 is indeed a possible answer for this case since we know that x ^–5/3 for this case.

For this case we know 3x+50,
we replace | 3x + 5 | by 3x + 5
to get 3x + 5 = 28
which is 3x = 23
which is x = 23/3
therefore, the answer is 23/3.
Note that 23/3 is indeed a possible answer for this case, since we know that x ^–5/3 for this case.

Putting the two cases together, we have the solution is the set
{ ^–11, 23/3 }

Problem 9

Solution

Find: | 4x – 9 | = 115

We do not know if 4x – 9 is negative, or non-negative.
We need to know this if we are going to use our definition.
We will break the problem into two cases, one where
4x – 9 is negative, and one where 4x – 9 is non-negative.

Case 1: 4x–9 0
which means, 4x 9
which means, x 9/4

Case 2: 4x–9 0
which means, 4x 9
which means, x 9/4

For this case we know 4x–90,
therefore, we replace | 4x – 9 | by ^–(4x–9)
this gives ^–(4x–9) = 115
which is the same as (^–1)(4x–9) = 115
which yields (^–1)4x – (^–1)9 = 115
or, simplifying, ^–4x + 9 = 115
or, simplifying, ^–4x = 106
which we solve to get x = ^–106/4 = ^–53/2
therefore, the answer is ^–53/2.
Note that ^–53/2 is indeed a possible answer for this case since we know that x 9/4 for this case.

For this case we know 4x–90,
we replace | 4x – 9 | by 4x – 9
to get 4x – 9 = 115
which is 4x = 124
which is x = 31
therefore, the answer is 31.
Note that 31 is indeed a possible answer for this case, since we know that x 9/4 for this case.

Putting the two cases together, we have the solution is the set
{ ^–53/2, 31 }

Problem 10

Solution

Find: | 7 – 5x | = 33

We do not know if 7 – 5x is negative, or non-negative.
We need to know this if we are going to use our definition.
We will break the problem into two cases, one where
7 – 5x is negative, and one where 7 – 5x is non-negative.

Case 1: 7 – 5x 0
which means, ^–5x ^–7
which means, x 7/5

Case 2: 7 – 5x 0
which means, ^–5x ^–7
which means, x 7/5

For this case we know 7 – 5x0,
therefore, we replace | 7 – 5x | by ^–(7 – 5x)
this gives ^–(7 – 5x) = 33
which is the same as (^–1)(7 – 5x) = 33
which yields (^–1)7 – (^–1)5x = 33
or, simplifying, ^–7 + 5x = 33
or, simplifying, 5x = 40
which we solve to get x = 8
therefore, the answer is 8.
Note that 8 is indeed a possible answer for this case since we know that x 7/5 for this case.

For this case we know 7 – 5x0,
we replace | 7 – 5x | by 7 – 5x
to get 7 – 5x = 33
which is ^–5x = 26
which is x = ^–26/5
therefore, the answer is ^–26/5.
Note that ^–26/5 is indeed a possible answer for this case, since we know that x 9 for this case.

Putting the two cases together, we have the solution is the set
{ ^–26/5, 8 }

Problem 11

Solution

Find: | x | 7

Case 1: x 0	Case 2: x 0
For this case we know x0, therefore, we replace \| x \| by ^–(x) this gives ^–(x) 7 which we solve to get x ^–7 therefore, the answer is x ^–7. Note that x^–7 is indeed a possible answer for this case because we already know that any solution for this case must have x0.	For this case we know x0, we replace \| x \| by x to get x 7 therefore, the answer is x7. Note that x7 is indeed a possible answer for this case because we already know that any solution for this case must have x0.

Putting the two cases together, we have the solution in set-builder notation:
{x|x ^–7} {x|x 7} or in interval notation: (, ^–7) (7, )

Problem 12

Solution

Find: | x | 13

Case 1: x 0	Case 2: x 0
For this case we know x0, therefore, we replace \| x \| by ^–(x) this gives ^–(x) 13 which we solve to get x ^–13 therefore, the answer is x ^–13. Note that x^–13 is indeed a possible answer for this case but only for values up to 0, because we already know that any solution for this case must have x0.	For this case we know x0, we replace \| x \| by x to get x 13 therefore, the answer is x 13. Note that x13 is indeed a possible answer for this case but only down to and including 0, because we already know that any solution for this case must have x0.

Putting the two cases together, we have the solution in set-builder notation:
{x|^–13 x 0} {x|0 x 13} which simplifies to: {x|^–13 x 13} or in interval notation: (^–13,0) [0,13) which simplifies to: (^–13, 13)

Problem 13

Solution

Find: | x + 5| 21

We do not know if x + 5 is negative, or non-negative.
We need to know this if we are going to use our definition.
We will break the problem into two cases, one where
x + 5 is negative, and one where x + 5 is non-negative.

Case 1: x + 5 0
which means x ^–5

Case 2: x +5 0
which means x ^–5

For this case we know x + 50,
therefore, we replace | x + 5 | by ^–(x+5)
this gives ^–(x + 5) 21
which becomes (^–1)(x + 5) 21
which becomes (^–1)(x) + (^–1)(5) 21
which becomes ^–x + ^–5 21
which becomes ^–x 26
which we solve to get x ^–26
therefore, the answer is x ^–26.
Note that x^–26 is indeed a possible answer for this case because we already know that any solution for this case must have x^–5.

For this case we know x + 50,
we replace | x +5| by x + 5
to get x + 5 21
which becomes x 16
therefore, the answer is x 16.
Note that x16 is indeed a possible answer for this case because we already know that any solution for this case must have x^–5.

Putting the two cases together, we have the solution in set-builder notation:
{x|x ^–26} {x|x 16} or in interval notation: (, ^–26] [16, )

Problem 14

Solution

Find: | x + 9 | 5

We do not know if x + 9 is negative, or non-negative.
We need to know this if we are going to use our definition.
We will break the problem into two cases, one where
x + 9 is negative, and one where x + 9 is non-negative.

Case 1: x + 9 0
which means x ^–9

Case 2: x + 9 0
which means x ^–9

For this case we know x+90,
therefore, we replace | x + 9 | by ^–(x + 9)
this gives ^–(x + 9) 5
which becomes (^–1)(x + 9) 5
which becomes (^–1)(x) + (^–1)(9) 5
which becomes ^–x + ^–9 5
which becomes ^–x 14
which we solve to get x ^–14
therefore, the answer is x ^–14.
Note that x^–14 is indeed a possible answer for this case but only for values up to ^–9, because we already know that any solution for this case must have x^–9.

For this case we know x + 90,
we replace | x + 9 | by x + 9
to get x + 9 5
which becomes x ^–4
therefore, the answer is x ^–4.
Note that x^–4 is indeed a possible answer for this case but only down to and including ^–9, because we already know that any solution for this case must have x^–9.

Putting the two cases together, we have the solution in set-builder notation:
{x|^–14 x ^–9} {x|^–9 x ^–4} which simplifies to: {x|^–14 x ^–4} or in interval notation: [^–14, ^–9) [^–9, ^–4] which simplifies to: [^–14, ^–4]

Problem 15

Solution

Find:
| 3x – 4| 5x – 12

We do not know if 3x – 4 is negative, or non-negative.
We need to know this if we are going to use our definition.
We will break the problem into two cases, one where
3x – 4 is negative, and one where 3x – 4 is non-negative.

Case 1: 3x – 4 0
which means x 4/3

Case 2: 3x – 4 0
which means x 4/3

For this case we know 3x – 4 0,
therefore, we replace | 3x – 4 | by ^–(3x – 4 )
this gives ^–(3x – 4 ) 5x – 12
which becomes (^–1)(3x – 4 ) 5x – 12
which becomes (^–1)(3x) – (^–1)(4) 5x – 12
which becomes ^–3x + 4 5x – 12
which becomes ^–8x ^–16
which we solve to get x 2
therefore, the answer is x 2.
Note that x2 is indeed a possible answer for this case because we already know that any solution for this case must have x4/3. Thus, for this case, all values x4/3 form the solution.

For this case we know 3x – 4 0,
we replace | 3x – 4 | by 3x – 4
to get 3x – 4 5x – 12
which becomes ^–2x ^–8
therefore, the answer is x 4.
Note that x4 is indeed a possible answer for this case because we already know that any solution for this case must have x 4/3.

Putting the two cases together, we have the solution in set-builder notation:
{x|x 4/3} {x| 4/3 x 4} which simplifies to {x|x 4} or in interval notation: (, 4/3) [4/3, 4] which simplifies to (, 4]

Problem 16

Solution

Find:
| 4x–13 | 8–x

We do not know if 4x–13 is negative, or non-negative.
We need to know this if we are going to use our definition.
We will break the problem into two cases, one where
4x–13 is negative, and one where 4x–13 is non-negative.

Case 1: 4x–13 0
which means x 13/4

Case 2: 4x–13 0
which means x 13/4

For this case we know 4x–130,
therefore, we replace | 4x–13 | by ^–(4x–13)
this gives ^–(4x–13) 8–x
which becomes (^–1)(4x–13) 8–x
which becomes (^–1)(4x) – (^–1)(13) 8–x
which becomes ^–4x + 13 8–x
which becomes ^–3x ^–5
which we solve to get x 5/3
therefore, the answer is x 5/3.
Note that x5/3 is indeed a possible answer for this case but only for values up to 13/4, because we already know that any solution for this case must have x13/4.

For this case we know 4x–130,
we replace | 4x–13 | by 4x–13
to get 4x–13 8–x
which becomes 5x 21
which we solve to get x 21/5
therefore, the answer is x 21/5.
Note that x21/5 is indeed a possible answer for this case but only down to and including 13/4, because we already know that any solution for this case must have x13/4.

Putting the two cases together, we have the solution in set-builder notation:
{x| 5/3 x 13/4} {x| 13/4 x 21/5} which simplifies to: {x| 5/3 x 21/5} or in interval notation: [5/3, 13/4) [13/4, 21/5] which simplifies to: [5/3, 21/5]