
 and
and  , but for the TI-86
we start with
, but for the TI-86
we start with  and
and  . On either calculator this selects the "SIMULT" function.
The calculator responds with a request for the
value of "Number" as shown in Figure 1. The SIMULT function expects to have exactly the
same number of equations as we have variables. For our problem, we have 7 variables
and 7 equations. Therefore we respond with the
. On either calculator this selects the "SIMULT" function.
The calculator responds with a request for the
value of "Number" as shown in Figure 1. The SIMULT function expects to have exactly the
same number of equations as we have variables. For our problem, we have 7 variables
and 7 equations. Therefore we respond with the  key to complete
Figure 1.
key to complete
Figure 1.

 key.
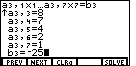
That will cause the display to change to Figure 2. Notice in Figure 2 that the
calculator is requesting values for each of the first six coefficients, using
the general standard form for our first equation.
The remaining coefficient and the constant value do not fit on the screen.
The down-arrow to the left of the a1,6 indicates that there are more entries for
this screen. Figure 2 also shows that we have supplied the values for the
first six coefficients from the first equation
key.
That will cause the display to change to Figure 2. Notice in Figure 2 that the
calculator is requesting values for each of the first six coefficients, using
the general standard form for our first equation.
The remaining coefficient and the constant value do not fit on the screen.
The down-arrow to the left of the a1,6 indicates that there are more entries for
this screen. Figure 2 also shows that we have supplied the values for the
first six coefficients from the first equation













 . After pressing
those keys the screen should appear as in Figure 2.
. After pressing
those keys the screen should appear as in Figure 2.

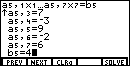
 key to move to the next data value. Figure 3 shows the
result of pressing that key. The calculator is now ready for the seventh coeffiicient
in the first equation.
key to move to the next data value. Figure 3 shows the
result of pressing that key. The calculator is now ready for the seventh coeffiicient
in the first equation.
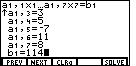
 , pressed
, pressed  to
move to the constant value, and entered 114 via the
to
move to the constant value, and entered 114 via the


 keys. This completes the first equation. We can press
keys. This completes the first equation. We can press
 to move to the next equation.
to move to the next equation. 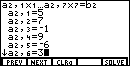












 keys.
We can move to the next coefficient via the
keys.
We can move to the next coefficient via the  key.
key.
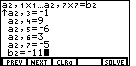





 keys.
We can press
keys.
We can press
 to move to the next equation.
to move to the next equation. 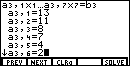












 keys.
We can move to the next coefficient via the
keys.
We can move to the next coefficient via the  key.
key.




 keys.
We can press
keys.
We can press
 to move to the next equation.
to move to the next equation. 











 keys.
We can move to the next coefficient via the
keys.
We can move to the next coefficient via the  key.
key.






 keys.
We can press
keys.
We can press
 to move to the next equation.
to move to the next equation. 













 keys.
We can move to the next coefficient via the
keys.
We can move to the next coefficient via the  key.
key.


 keys.
We can press
keys.
We can press
 to move to the next equation.
to move to the next equation. 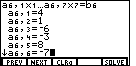













 keys.
We can move to the next coefficient via the
keys.
We can move to the next coefficient via the  key.
key.






 keys.
We can press
keys.
We can press
 to move to the last equation.
to move to the last equation. 












 keys.
We can move to the next coefficient via the
keys.
We can move to the next coefficient via the  key.
key.






 keys.
We are ready to "solve" the system of linear equations.
keys.
We are ready to "solve" the system of linear equations. 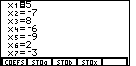
 key to select the "SOLVE" option from the
menu. The calculator responds with the solution shown in Figure 17.
key to select the "SOLVE" option from the
menu. The calculator responds with the solution shown in Figure 17.
This is the solution to the equations that we have entered via the coefficients and the constants. We recall that x1 is s, x2 is t, x3 is u, x4 is v, x5 is w, x6 is x, and x7 is y. Therefore, the values s=5, t=-7, u=8, v=-6, w=-9, x=2, and y=-3 solve all seven equations.
 , while on the TI-86 it is
, while on the TI-86 it is
 . To save some space, and to ignore this difference, the numeric keys
(the gray ones) have been changed here to only show the key
face, as in
. To save some space, and to ignore this difference, the numeric keys
(the gray ones) have been changed here to only show the key
face, as in  key will be shown as
key will be shown as