We are looking for the values of the variables that make all four equations true.
Figure 1
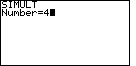
|
The keystrokes to start this process are the same on the two calculators, although
the keys have a different name. For the TI-85 we start with  and
and  , but for the TI-86
we start with , but for the TI-86
we start with  and
and  . On either calculator this selects the "SIMULT" function.
The calculator responds with a request for the
value of "Number" as shown in Figure 1. The SIMULT function expects to have exactly the
same number of equations as we have variables. For our problem, we have 4 variables
and 4 equations. Therefore we respond with the . On either calculator this selects the "SIMULT" function.
The calculator responds with a request for the
value of "Number" as shown in Figure 1. The SIMULT function expects to have exactly the
same number of equations as we have variables. For our problem, we have 4 variables
and 4 equations. Therefore we respond with the  key to complete
Figure 1. key to complete
Figure 1. |
Figure 2

| We leave Figure 1 by pressing the  key.
That will cause the display to change to Figure 2.
In that figure we have also entered the desired values,
3, 5, 2, 7, and 10, via the key.
That will cause the display to change to Figure 2.
In that figure we have also entered the desired values,
3, 5, 2, 7, and 10, via the
 
 
 
  
 and
and  keys. keys.
|
Figure 3
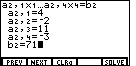
| We leave Figure 2 by pressing the  key.
That will cause the display to change to Figure 3.
In that figure we have also entered the desired values,
4, -2, 11, -3, and 71, via the key.
That will cause the display to change to Figure 3.
In that figure we have also entered the desired values,
4, -2, 11, -3, and 71, via the
 
  
  
  
 and and  keys.
After pressing
those keys the screen should appear as in Figure 3. keys.
After pressing
those keys the screen should appear as in Figure 3. |
Figure 4
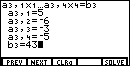
| We accept the values of Figure 3 and move to Figure 4 by pressing the
 key.
That will cause the display to change to Figure 4.
In that figure we have also entered the desired values,
5, -6, -3, -5, and 43, via the key.
That will cause the display to change to Figure 4.
In that figure we have also entered the desired values,
5, -6, -3, -5, and 43, via the
 
  
  
  
 and and  keys.
After pressing
those keys the screen should appear as in Figure 4. keys.
After pressing
those keys the screen should appear as in Figure 4.
|
Figure 5
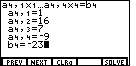
| The values for the coefficients and constant in the fourth equation are
1, 16, 7, -9, and 23. We press
 
  
 
  
 and
and  to produce the display shown in Figure 5.
At this point we are ready to ask the calculator to solve the
problem. to produce the display shown in Figure 5.
At this point we are ready to ask the calculator to solve the
problem.
|
Figure 6

| We press the
 key, and the calculator responds with the error
message in Figure 6. This message means that there is no unique solution.
There may be an infinite set of values that work, or there may be no values that
work. In either case, we do not have a unique soltuion. key, and the calculator responds with the error
message in Figure 6. This message means that there is no unique solution.
There may be an infinite set of values that work, or there may be no values that
work. In either case, we do not have a unique soltuion.
|
If we go back tot he original problem, we may be able to see why there is no
unique solution. The original statement of the equations was:
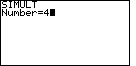
 and
and  , but for the TI-86
we start with
, but for the TI-86
we start with  and
and  . On either calculator this selects the "SIMULT" function.
The calculator responds with a request for the
value of "Number" as shown in Figure 1. The SIMULT function expects to have exactly the
same number of equations as we have variables. For our problem, we have 4 variables
and 4 equations. Therefore we respond with the
. On either calculator this selects the "SIMULT" function.
The calculator responds with a request for the
value of "Number" as shown in Figure 1. The SIMULT function expects to have exactly the
same number of equations as we have variables. For our problem, we have 4 variables
and 4 equations. Therefore we respond with the  key to complete
Figure 1.
key to complete
Figure 1.
 key.
That will cause the display to change to Figure 2.
In that figure we have also entered the desired values,
3, 5, 2, 7, and 10, via the
key.
That will cause the display to change to Figure 2.
In that figure we have also entered the desired values,
3, 5, 2, 7, and 10, via the









 and
and  keys.
keys.

 key.
That will cause the display to change to Figure 3.
In that figure we have also entered the desired values,
4, -2, 11, -3, and 71, via the
key.
That will cause the display to change to Figure 3.
In that figure we have also entered the desired values,
4, -2, 11, -3, and 71, via the











 and
and  keys.
After pressing
those keys the screen should appear as in Figure 3.
keys.
After pressing
those keys the screen should appear as in Figure 3. 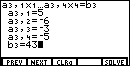
 key.
That will cause the display to change to Figure 4.
In that figure we have also entered the desired values,
5, -6, -3, -5, and 43, via the
key.
That will cause the display to change to Figure 4.
In that figure we have also entered the desired values,
5, -6, -3, -5, and 43, via the











 and
and  keys.
After pressing
those keys the screen should appear as in Figure 4.
keys.
After pressing
those keys the screen should appear as in Figure 4.











 and
and  to produce the display shown in Figure 5.
At this point we are ready to ask the calculator to solve the
problem.
to produce the display shown in Figure 5.
At this point we are ready to ask the calculator to solve the
problem.

 key, and the calculator responds with the error
message in Figure 6. This message means that there is no unique solution.
There may be an infinite set of values that work, or there may be no values that
work. In either case, we do not have a unique soltuion.
key, and the calculator responds with the error
message in Figure 6. This message means that there is no unique solution.
There may be an infinite set of values that work, or there may be no values that
work. In either case, we do not have a unique soltuion.
 , while on the TI-86 it is
, while on the TI-86 it is
 . To save some space, and to ignore this difference, the numeric keys
(the gray ones) have been changed here to only show the key
face, as in
. To save some space, and to ignore this difference, the numeric keys
(the gray ones) have been changed here to only show the key
face, as in  key will be shown as
key will be shown as