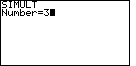
 and
and  , but for the TI-86
we start with
, but for the TI-86
we start with  and
and  . On either calculator this selects the "SIMULT" function.
The calculator responds with a request for the
value of "Number" as shown in Figure 1. The SIMULT function expects to have exactly the
same number of equations as we have variables. For our problem, we have 3 variables
and 4 equations. Therefore we respond with the
. On either calculator this selects the "SIMULT" function.
The calculator responds with a request for the
value of "Number" as shown in Figure 1. The SIMULT function expects to have exactly the
same number of equations as we have variables. For our problem, we have 3 variables
and 4 equations. Therefore we respond with the  key to complete
Figure 1.
key to complete
Figure 1.
 key.
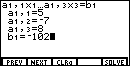
The calculator shifts to the screen in Figure 2, asking for the
coefficients and constant value for the first equation. The key sequence
key.
The calculator shifts to the screen in Figure 2, asking for the
coefficients and constant value for the first equation. The key sequence










 enters
those values and completes Figure 2.
enters
those values and completes Figure 2.
 key.
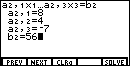
The calculator shifts to the screen in Figure 3, asking for the
coefficients and constant value for the second equation. The key sequence
key.
The calculator shifts to the screen in Figure 3, asking for the
coefficients and constant value for the second equation. The key sequence








 enters
those values and completes Figure 3.
enters
those values and completes Figure 3.
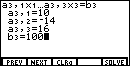
Now we can move to the next screen by
pressing the  key.
key.












 to
complete the image of Figure 4.
to
complete the image of Figure 4.
We have entered all of the values. We are ready to solve the system of linear equations.

 key.
The calculator displays the error message in Figure 5.
key.
The calculator displays the error message in Figure 5.
We could press  to quit the SIMULT processing, or
we could press
to quit the SIMULT processing, or
we could press  to return to the data entry phase of
the SIMULT processing, giving us a display that is essentially the same
as was given in Figure 2. We would do this so that we could display and change if need be the
coefficients and constant terms. In this case, the values were entered correctly.
We could simply quit the processing.
to return to the data entry phase of
the SIMULT processing, giving us a display that is essentially the same
as was given in Figure 2. We would do this so that we could display and change if need be the
coefficients and constant terms. In this case, the values were entered correctly.
We could simply quit the processing.
 , while on the TI-86 it is
, while on the TI-86 it is
 . To save some space, and to ignore this difference, the numeric keys
(the gray ones) have been changed here to only show the key
face, as in
. To save some space, and to ignore this difference, the numeric keys
(the gray ones) have been changed here to only show the key
face, as in  key will be shown as
key will be shown as