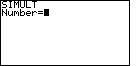
 and
and  , but for the TI-86
we start with
, but for the TI-86
we start with  and
and  . On either calculator this selects the "SIMULT" function.
The calculator responds with a request for the
value of "Number" as shown in Figure 1. The SIMULT function expects to have exactly the
same number of equations as we have variables. For our problem, we have 2 variables
and 2 equations.
. On either calculator this selects the "SIMULT" function.
The calculator responds with a request for the
value of "Number" as shown in Figure 1. The SIMULT function expects to have exactly the
same number of equations as we have variables. For our problem, we have 2 variables
and 2 equations.
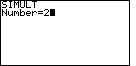
Since we have 2 variables and 2 equations, we respond with the value 2 by
pressing the  key. This is shown in Figure 2.
Then we conclude our input with the
key. This is shown in Figure 2.
Then we conclude our input with the  key.
key.
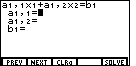
3x + 4y = 14 so we will want to respond with the value 3.

 key followed by the
key followed by the  key.
Notice that the blinking cursor has moved to the next line, asking for a value
for a1,2 which is the coefficient for the
second variable in the first equation.
key.
Notice that the blinking cursor has moved to the next line, asking for a value
for a1,2 which is the coefficient for the
second variable in the first equation.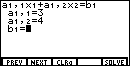
 key.
Then we could press the "enter" button as we did in Figure 4. However, we
could also press the
key.
Then we could press the "enter" button as we did in Figure 4. However, we
could also press the  key and have the same effect,
as shown in Figure 5.
key and have the same effect,
as shown in Figure 5.
This leaves the calculator asking for the value of b1, the constant term in the first equation.
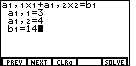
3x + 4y = 14 so we will want to respond with the value 14. The keys

 produce this value and
change the display to Figure 6.
produce this value and
change the display to Figure 6. We have entered all of the values for the first equation. Now, if we press either the "enter" or the "down arrow" key, the calculator will display a new screen asking for values for the second equation.
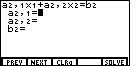
 key. The display in Figure 7 is asking for the coefficients and constant for the
second equation.
Notice that a2,1 is the coefficient of the first variable in the second equation,
a2,2 is the coefficient of the second variable in the second equation. And,
b2 is the constant value in the second equation. We are ready to assign
values to those items.
key. The display in Figure 7 is asking for the coefficients and constant for the
second equation.
Notice that a2,1 is the coefficient of the first variable in the second equation,
a2,2 is the coefficient of the second variable in the second equation. And,
b2 is the constant value in the second equation. We are ready to assign
values to those items.
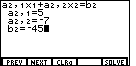






 and
and
 . The calculator display should appear as in Figure 8, with the
blinking cursor following the -45.
. The calculator display should appear as in Figure 8, with the
blinking cursor following the -45.
At this point we are done entering all of th evalues for the two equations. We could just select the "SOLVE" option from the menu at this point. However, there is a tendency to press the "ENTER" key to signal the "end of data". Doing so will do no harm and is shown in Figure 9.

 key at the end of Figure 8
is shown in Figure 9. The blinking cursor returns to the start of the data entry field for
the last value. In our case, the cursor is positioned over the negative sign of the -45.
This change does not affect the values already entered.
key at the end of Figure 8
is shown in Figure 9. The blinking cursor returns to the start of the data entry field for
the last value. In our case, the cursor is positioned over the negative sign of the -45.
This change does not affect the values already entered.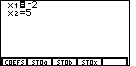
 key. The calculator responds with the
data in Figure 10, namely that the solution is x1=-2
and x2=-5.
Remember that x1 corresponds to the variable x in the
original problem. Similarly, x2 corresponds to the variable
y. Therefore, the solution is x=-2 and y=5,
or, as an ordered pair, the point (-2,5).
key. The calculator responds with the
data in Figure 10, namely that the solution is x1=-2
and x2=-5.
Remember that x1 corresponds to the variable x in the
original problem. Similarly, x2 corresponds to the variable
y. Therefore, the solution is x=-2 and y=5,
or, as an ordered pair, the point (-2,5).
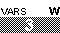 , while on the TI-86 it is
, while on the TI-86 it is
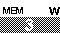 . To save some space, and to ignore this difference, the numeric keys
(the gray ones) have been changed here to only show the key
face, as in
. To save some space, and to ignore this difference, the numeric keys
(the gray ones) have been changed here to only show the key
face, as in  key will be shown as
key will be shown as