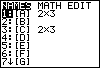With all of that out of the way, we are finally ready to start using the calculator.
The steps shown before assume that the calculator is turned on, that we are not in any
menu, and that the screen is clear.
Figure 1

| In Figure 1 we enter the desired matrix directly from the calculator keyboard.
To do this we use the   to generate a [
to signal the start of the matrix. A second to generate a [
to signal the start of the matrix. A second   produces a [ to signal the start of a row. Then we give the coeeficients and the constant of
the row, separated by commas. The keys for our example are
produces a [ to signal the start of a row. Then we give the coeeficients and the constant of
the row, separated by commas. The keys for our example are
 
 

 .
Then we use .
Then we use   and
and   to produce ][
to signal the end of the first row and the start of the second row, respectively. The
values in the second row are to produce ][
to signal the end of the first row and the start of the second row, respectively. The
values in the second row are  
  
 
 .
Then, we need to end the second row with a ], and end the matrix with a ].
We do this with the keys .
Then, we need to end the second row with a ], and end the matrix with a ].
We do this with the keys   and
and   .
Finally, we want to store this matrix on the calculator. We start to store it
by pressing the .
Finally, we want to store this matrix on the calculator. We start to store it
by pressing the  key. key.
|
Figure 2

| On a TI-83 or a TI-83 Plus we need to store a matrix into one of the 10 predefined matrices,
[A], [B], [C], [D], [E], [F], [G], [H], [I], or [J]. To do this we need to find
the name of the desired matrix. The names are available in the MATRIX menu. On the TI-83 we press the
 key to open the MATRIX menu. (As noted at the start of this page,
on the TI-83 Plus we use the sequence key to open the MATRIX menu. (As noted at the start of this page,
on the TI-83 Plus we use the sequence   keys to accomplish the same thing.)
Figure 2 shows the MATRIX menu. The calculator used here already has a matrix stored in [A],
in fact it has a matrix with 10 rows and 7 columns stored in [A]. We will store our matrix in place of that
one. To do this, we can press the keys to accomplish the same thing.)
Figure 2 shows the MATRIX menu. The calculator used here already has a matrix stored in [A],
in fact it has a matrix with 10 rows and 7 columns stored in [A]. We will store our matrix in place of that
one. To do this, we can press the  key to select the [A] matrix name. key to select the [A] matrix name.
|
Figure 3

| Figure 3 shows the result of our work in Figure 2. The name [A] has been appended to the store command
in our screen. The action has not been performed at this point. We have merely created the
command that defines the matrix and assigns it to [A]. To perform that command we press the
 key. key.
|
Figure 4

| Having performed the command to leave Figure 3 the calculator stores the matrix into [A] and
then displays it on the screen as  This is the form that the TI-83 uses to display a matrix.
This is the form that the TI-83 uses to display a matrix.
|
Figure 5

| Our next step is to find the reduced row echelon form of this matrix.
We could do this ourselves, using what are known as
elementary row operations. However, the TI-83
has a function that will try to produce the reduced row echelon form of the original matrix.
That command is rref(). We can find this command in the MATRIX menu. Therefore,
we open that menu again, via the  key. The result is shown in Figure 5.
Note that [A] shows up in the list of matrix names as having 2 rows and 3 columns. key. The result is shown in Figure 5.
Note that [A] shows up in the list of matrix names as having 2 rows and 3 columns.
|
Figure 6

| Our rref() function is not in the list of names. Rather, we will find it under the MATH option.
Therefore, we press the  key to move the highlight at the top onto the MATH option, as shown in
Figure 6. Now we have a new list of options on the screen. Unfortunately,
rref() is not one of them. Therefore, use the key to move the highlight at the top onto the MATH option, as shown in
Figure 6. Now we have a new list of options on the screen. Unfortunately,
rref() is not one of them. Therefore, use the  key to move the
selection highlight down the screen until it the screen appears as shown in Figure 7. key to move the
selection highlight down the screen until it the screen appears as shown in Figure 7.
|
Figure 7

| In Figure 7 we have located the rref( function. Press  to select that option
and paste rref( onto the main screen. to select that option
and paste rref( onto the main screen.
|
Figure 8
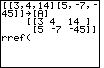
| The full command that we want to construct is rref([A]).
In Figure 8 we have the start of this command. Now we need to append the name of our matrix.
To do this we will need to open the MATRIX menu again. Press
 to move to Figure 9. to move to Figure 9.
|
Figure 9

| Once again, the list of matrix names is presented. [A] is already highlighted.
Therefore, we can press  to select [A] and move to Figure 10. to select [A] and move to Figure 10.
|
Figure 10

| Once [A] has been pasted into the command,
we press  to cpomplete the
comamnd, as shown in Figure 10. All that remains is to press to cpomplete the
comamnd, as shown in Figure 10. All that remains is to press  to get the calculator to
perform the function and to produce the reduced row echelon form of the original matrix [A]. to get the calculator to
perform the function and to produce the reduced row echelon form of the original matrix [A].
|
Figure 11
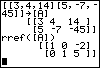
| Finally, we have the reduced row echolon form of the original matrix. This new form appears as
 remember that this is merely a shorthand version of the two linear equations
1X + 0Y = – 2
remember that this is merely a shorthand version of the two linear equations
1X + 0Y = – 2
0X + 1Y = 5
and those equations tell us that X=– 2 while Y=5.
That point, the point (– 2,5), is the solution to the original problem.
|
The first 11 Figures on this page demonstated a calculator solution to the given problem.
This solution required us to create a matrix to hold the coeeficients and the constants of the
two equations. We created that matrix by typing it into the calculator, back in Figure 1, and then storing it into
a matrix variable in Figure 2 and 3. There is an alternate method to enter or change a matrix, namely, we can
use the matrix editor.
Figures 12 through 22 demonstrate using the matrix editor to
enter a new matrix into the
matrix variable [C].
The new matrix will represent the two equations
Figure 12
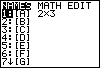
| We open the matrix menu by pressing the
 key. key.
|
Figure 13
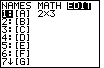
| Next we press   to move the
highlight to the EDIT menu item.
In Figure 13 we note that the highlight has moved, and that [A] is selected. We want to
select [C]. to move the
highlight to the EDIT menu item.
In Figure 13 we note that the highlight has moved, and that [A] is selected. We want to
select [C].
|
Figure 14

| The key sequence   moves the selection highlight to
our desired [C]. Press moves the selection highlight to
our desired [C]. Press  to move to Figure 15. to move to Figure 15.
|
Figure 15
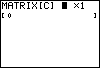
| Here the calculator has opened the matrix [C]
in the matrix editor. At the moment this is a 1 row and 1 column matrix, and the one element
in it is 0. However, the flashing cursor is on the number of rows in the matrix.
|
Figure 16
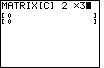
| In Figure 16 we have changed the number of rows in the matrix to 2 by typing
  and we have started
to change the number of columns to 3 by typing and we have started
to change the number of columns to 3 by typing  . The screen already
shows the two rows, but it has not changed to chow 3 columns. We will need to
press . The screen already
shows the two rows, but it has not changed to chow 3 columns. We will need to
press  again to do this and move to Figure 17. again to do this and move to Figure 17.
|
Figure 17
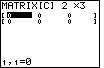
| Both rows and all three columns are visible in the display. The cursor is
on item 1,1 which currently holds 1. We want to have that item be 4. Therefore,
we press the  key to move to Figure 18. key to move to Figure 18.
|
Figure 18
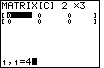
| Note that the new value is being formed at the bottom of the screen,
but that it has not yet been assigned to the element of the matrix. To signal the
end of the number and to have the value placed into the matrix, we press
 , and move on to Figure 19. , and move on to Figure 19.
|
Figure 19
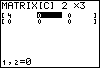
| Our 4 is in the correct place. THe highlight is on the element
in the first row, second column.
At the bottom of the screen we see that the current value is 0. We want
it to be – 3.
We press   to enter that value
at the bottom of the screen, shown in Figure 20. to enter that value
at the bottom of the screen, shown in Figure 20.
|
Figure 20
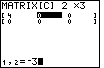
| The – 3 value is shown at the bottom. Press
 top accept that value and move on to the
next matrix element. Thereafter, we continue to enter array elements
until we have the values shown in Figure 21. top accept that value and move on to the
next matrix element. Thereafter, we continue to enter array elements
until we have the values shown in Figure 21.
|
Figure 21

| Figure 21 reflects the steps taken to enter the matrix, up to but
not inlcuding the entry of the final value, – 50, into the
element at row 2 column 3. Once we press  to complete
the entry of this value, our matrix will be
complete. to complete
the entry of this value, our matrix will be
complete.
|
Figure 22
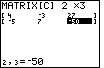
| Here we have the completed matrix. Note that the highlight is still on the
element in the lst row, last column. We could use the cursor keys to move around
within the matrix. Right now we will verify that
all of the values in the matrix are correct.
|
Figure 23
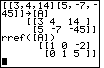
| Once we are satisfied that hte matrix holds the correct values,
we press the sequence   to exit the matrix editor.
This retuns us to the main screen, which is unchanged since we left after Figure 11. We need to
formulate the rref([C]) command. To do this we press to exit the matrix editor.
This retuns us to the main screen, which is unchanged since we left after Figure 11. We need to
formulate the rref([C]) command. To do this we press
 to open the matrix menu, shown in Figure 24. to open the matrix menu, shown in Figure 24.
|
Figure 24

| We use the  key to move the highlight to the MATH menu option. key to move the highlight to the MATH menu option.
|
Figure 25

| Use  over and over until we have the selector highlight
on the rref( function.
Press over and over until we have the selector highlight
on the rref( function.
Press  to paste that
selection onto the main screen, shown in Figure 26. to paste that
selection onto the main screen, shown in Figure 26.
|
Figure 26

| The command has been started. We need to generate the name of our matrix, C,
so we press  to open the matrix menu again, as shown in Figure 27. to open the matrix menu again, as shown in Figure 27.
|
Figure 27
| We can select the [C] item by pressing the  key.
That will paste [C] onto the main screen. key.
That will paste [C] onto the main screen.
|
Figure 28

| We complete the command with   and the calculator responds as in Figure 28.
The matrix that we put into [C] represented the two equations
4x – 3y = 27
and the calculator responds as in Figure 28.
The matrix that we put into [C] represented the two equations
4x – 3y = 27
– 5x + 7y = – 50
The reduced row echelon form represents the two equations
1x + 0y = 3
0x + 1y = – 5
That is, x=3 and y=– 5.
|


 to generate a [
to signal the start of the matrix. A second
to generate a [
to signal the start of the matrix. A second 
 produces a [ to signal the start of a row. Then we give the coeeficients and the constant of
the row, separated by commas. The keys for our example are
produces a [ to signal the start of a row. Then we give the coeeficients and the constant of
the row, separated by commas. The keys for our example are





 .
Then we use
.
Then we use 
 and
and 
 to produce ][
to signal the end of the first row and the start of the second row, respectively. The
values in the second row are
to produce ][
to signal the end of the first row and the start of the second row, respectively. The
values in the second row are 






 .
Then, we need to end the second row with a ], and end the matrix with a ].
We do this with the keys
.
Then, we need to end the second row with a ], and end the matrix with a ].
We do this with the keys 
 and
and 
 .
Finally, we want to store this matrix on the calculator. We start to store it
by pressing the
.
Finally, we want to store this matrix on the calculator. We start to store it
by pressing the  key.
key.

 key to open the MATRIX menu. (As noted at the start of this page,
on the TI-83 Plus we use the sequence
key to open the MATRIX menu. (As noted at the start of this page,
on the TI-83 Plus we use the sequence 
 keys to accomplish the same thing.)
Figure 2 shows the MATRIX menu. The calculator used here already has a matrix stored in [A],
in fact it has a matrix with 10 rows and 7 columns stored in [A]. We will store our matrix in place of that
one. To do this, we can press the
keys to accomplish the same thing.)
Figure 2 shows the MATRIX menu. The calculator used here already has a matrix stored in [A],
in fact it has a matrix with 10 rows and 7 columns stored in [A]. We will store our matrix in place of that
one. To do this, we can press the  key to select the [A] matrix name.
key to select the [A] matrix name.

 key.
key.


 key. The result is shown in Figure 5.
Note that [A] shows up in the list of matrix names as having 2 rows and 3 columns.
key. The result is shown in Figure 5.
Note that [A] shows up in the list of matrix names as having 2 rows and 3 columns.

 key to move the highlight at the top onto the MATH option, as shown in
Figure 6. Now we have a new list of options on the screen. Unfortunately,
rref() is not one of them. Therefore, use the
key to move the highlight at the top onto the MATH option, as shown in
Figure 6. Now we have a new list of options on the screen. Unfortunately,
rref() is not one of them. Therefore, use the  key to move the
selection highlight down the screen until it the screen appears as shown in Figure 7.
key to move the
selection highlight down the screen until it the screen appears as shown in Figure 7.

 to select that option
and paste rref( onto the main screen.
to select that option
and paste rref( onto the main screen.

 to move to Figure 9.
to move to Figure 9.

 to select [A] and move to Figure 10.
to select [A] and move to Figure 10.

 to cpomplete the
comamnd, as shown in Figure 10. All that remains is to press
to cpomplete the
comamnd, as shown in Figure 10. All that remains is to press  to get the calculator to
perform the function and to produce the reduced row echelon form of the original matrix [A].
to get the calculator to
perform the function and to produce the reduced row echelon form of the original matrix [A].

 , again to save space.
, again to save space.
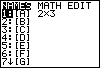
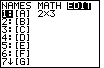

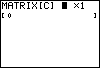
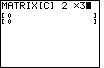

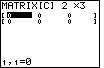
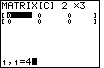
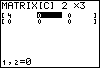
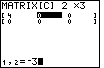

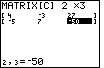

 to exit the matrix editor.
This retuns us to the main screen, which is unchanged since we left after Figure 11. We need to
formulate the rref([C]) command. To do this we press
to exit the matrix editor.
This retuns us to the main screen, which is unchanged since we left after Figure 11. We need to
formulate the rref([C]) command. To do this we press